光子学设计基础：夫琅和费衍射的理论与分析

在2.5节介绍过，波前上的每一点都可以正式而精确地看成是发出球面波的光源，在2.7节介绍过，两束光波叠加将会发生干涉。波前可以自身相干涉，或者与其他波干涉。通常，前者称为“衍射”，后者称为“干涉”。当然，对两者的区别稍微有些武断，在某些情况下并非能够分得如此清楚。

光的衍射可以看成是光源间隔变得无限小情况下发生干涉的极限情况。参看图2.21所示的狭缝孔径的情况：一束均匀的平面波照射该狭缝，在距离狭缝足够远的屏幕上观察通过狭缝的光，这样投射到屏幕上的光完全又成为平面波。这就是夫琅和费（Fraunhofer，或译为弗劳恩霍夫）衍射的条件。如果光源和屏幕到狭缝足够近，使光波不再是平面波，则会有比较复杂的情况，称为菲涅尔（Fresnel）衍射。到目前为止，夫琅和费衍射是比较重要的一种衍射，并且是在此要介绍的惟一一种衍射形式。通常，在各种情况下，都可以通过使用透镜将菲涅尔衍射转换成夫琅和费衍射，即使在很短的距离内，透镜也可以有效地将这种光波还原成平面波。

假设，图2.21所示的沿狭缝方向在x和x+dx之间波的振幅是一个复数量f（x）dx，现在来研究角度θ时的影响。波前上的每一点都可以看作是一个球面波的光源，当然，所有角度都会受到狭缝的照明。距离狭缝无穷远的屏幕上的一点将会受到狭缝上以θ和θ+dθ角度范围内出射光线的照射。以狭缝底部作为相位基准，那么到达屏幕上的光将会超前一个相位有

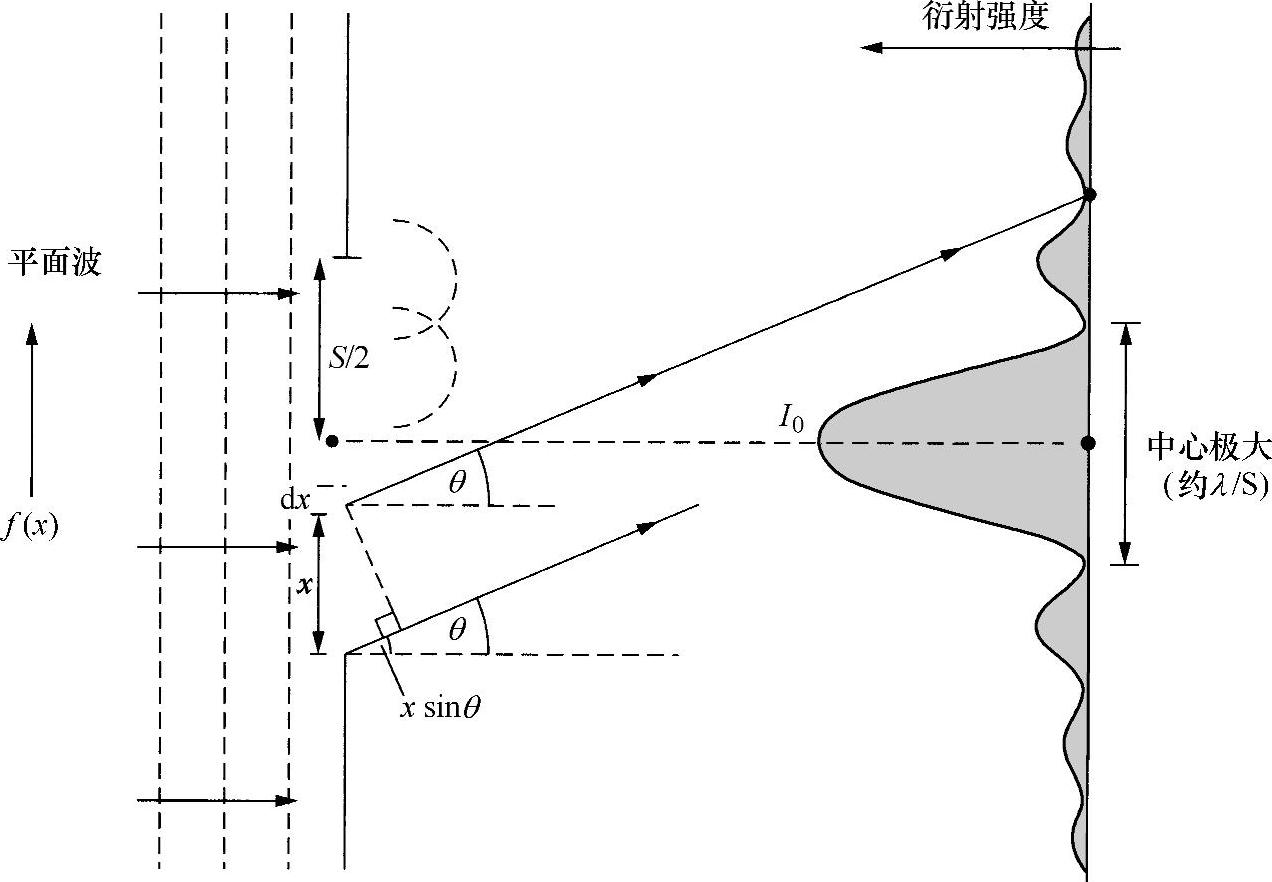
图2.21　狭缝衍射

Φ=kxsinθ

因此，在θ到θ+dθ方向上的总振幅为

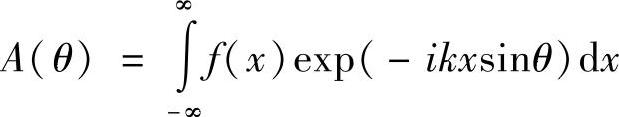
还可以写为

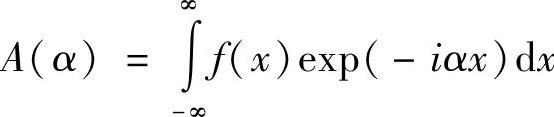
式中

α=ksinθ

因此，A（α）和f（x）组成逆傅里叶（Fourier）变换对（见附录Ⅱ）。就是说，每一个都是另一个的傅里叶变换，这是一个非常重要的结果。如果θ较小，这意味着，衍射光的角分布是孔径振幅分布的傅里叶变换。

现在就针对一些简单的例子，介绍是如何运算的。首先，假设宽度为s的狭缝受到均匀照明，衍射光的角分布为

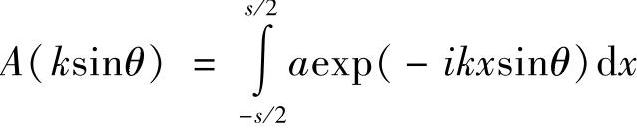
式中，a为狭缝处单位狭缝宽度的（均匀）振幅。因此有：

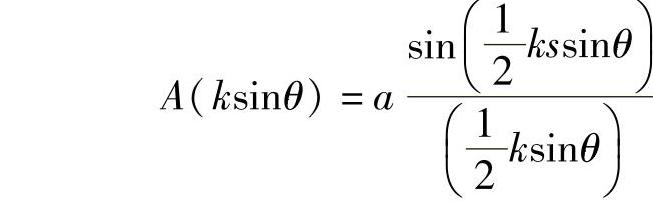
为了方便，使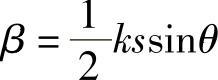，便得到θ方向的光强度为

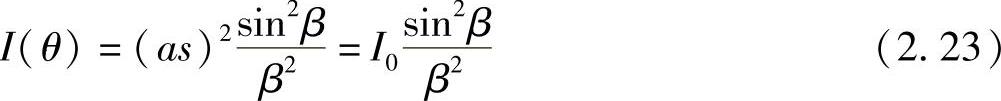
式中，I₀为衍射图中心的光强度。该变化如图2.21所示。并且，与离散光源之间多光束干涉的情况一样，其合成相位是那些相位规律地随θ增大的波矢量叠加的结果。

在许多应用中，这种形式的变量经常从物理学角度加以解释。这有益于理解其形成原因。适合于这种变量的函数是“sinc”（发音是sink），即

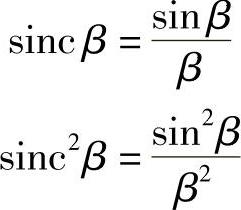
现在，讨论sinc函数在前面已经讨论过的情况（即均匀照明的狭缝）下的物理意义。在这种情况下，每一个无穷小狭缝元的波振幅是adx。并且，所有狭缝元在屏幕中心都是同相，因而得到的总振幅为as。因此，有可能将所有的这些基元矢量表示为长度as的一条直线（因为它们都是同相的）。下面讨论与轴线成θ角的情况。正如已经知道的，狭缝底部发出的光线比顶部发出的光线延迟一个相位，即

φ_T=kssinθ=2β

所以，可以如图2.22b所示那样描述该结果。第一个和最后一个无限小矢量彼此形成2β角度，其间矢量形成一个圆弧，对圆心的张角为2β。因此，所有矢量相加，得到一个合成矢量，就是图2.22b所示那段弧的弦，简单的几何运算就可以给出弦长：

A（θ）=2rsinβ （2.24）

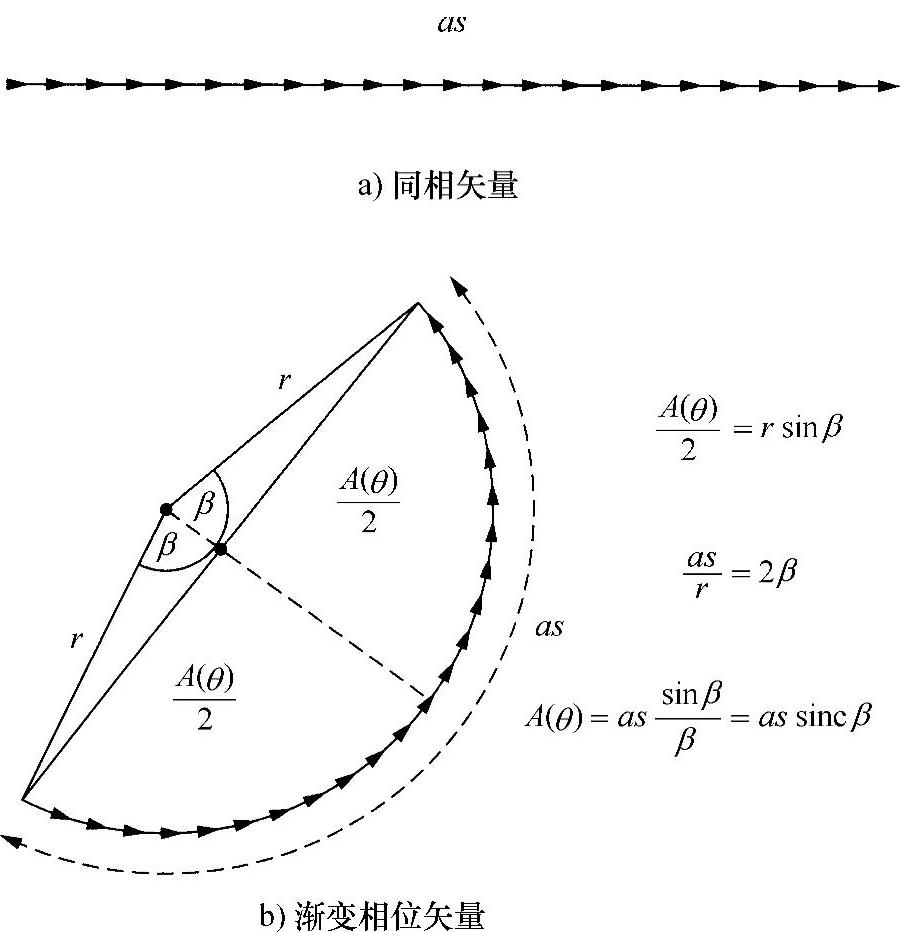
图2.22　sinc函数

式中，r为圆的半径。若所有矢量都同相，弧的总长与直线长度是一样的（即as），因此有：

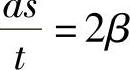
替代式（2.24）中的r，有：

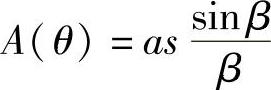(www.xing528.com)

因此，角度θ时的合成强度为

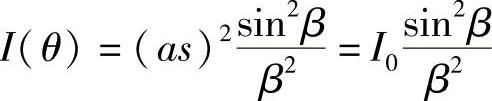
与式（2.23）一样。

物理学中普遍使用该变量的原因是，在大量无限小矢量中，常会遇到一些系统地增大相位差的现象，如光学干涉、电子干涉、质谱仪能量、粒子散射等。

导致使用sinc函数的原因是一样的，就是刚才阐述的那些原理。

现在，再返回来看一个狭缝的强度衍射图：

这种变量的一个重要性质是角发散度，当

成立时，主极大（θ=0）两侧立刻出现两个极小值，并有：

所以，如果θ比较小，中心极大的宽度就为

因此，在给定波长下，s越小，光能量发散越快，反之亦然。对于光学系统总的性能，这是一个重要的决定性因素。

作为第二个例子，讨论孔径范围内振幅的正弦变化。正弦曲线的傅里叶变换是由原点周围等间隔分布的一个正“频率”和一个负“频率”组成的。因此，衍射图恰好由观察屏中心位置附近等间隔分布的两条强度线组成（见图2.23）。可以对两个强度线照相，以证明是一个具有正弦衍射（干涉？）图的“双缝”孔径板。然而，该衍射图被视为“强度”图，而不是“振幅”图。因此它不包含，为了在衍射图中恰好产生两条线而必须要有正、负振幅的原始孔径。该例子不仅很好地说明了两种函数间的密切关系，而且强调，当所观察的衍射图（没有特定的方案布局）是强度函数时，反映的也是振幅函数间的关系。

最后讨论所有例子中最重要的一个：矩形波孔径振幅函数，如图2.24所示。这等效于一组窄狭缝，就是说，等效于一个衍射光栅。其傅里叶变换（和夫琅和费衍射图）是一组离散且均匀分布的、与孔径函数的“基频”一致并被一个狭缝的傅里叶变换所包络的强度线。如果孔径函数在任意方向都延伸到无穷远，那么每根线都是无限窄（δ函数）的。但是，实际上不可能做到这一点，其宽度反比于光栅的总宽度（就是说，对于矩形波，一条线上的强度分布基本上是包络函数的傅里叶变换）。

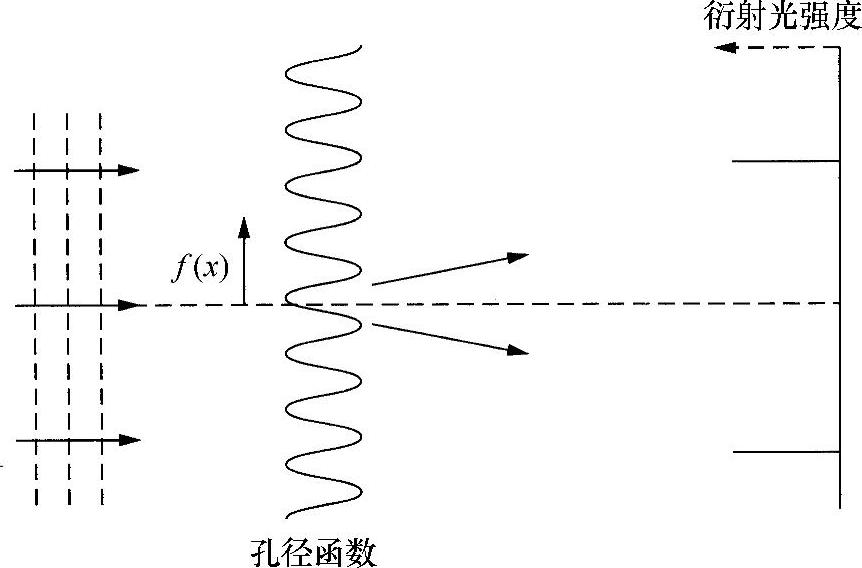
图2.23　正弦衍射孔径

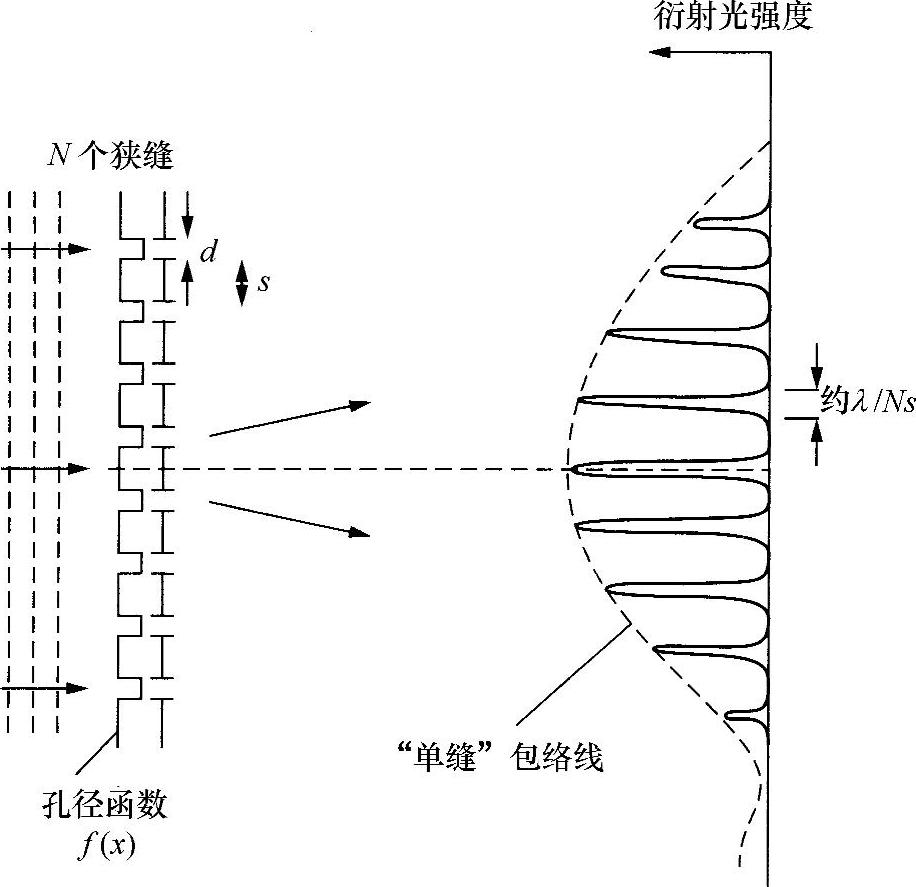
图2.24　衍射光栅

为了证实这些想法，现在讨论由N个狭缝组成的光栅，每个狭缝的宽度为d，狭缝间的距离为s。衍射后的光强度图为

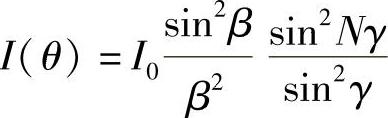
式中

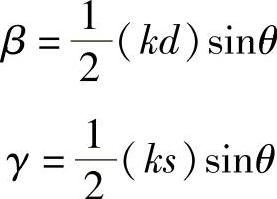
该衍射图如图2.24所示。正如所预料的，由于这是一种多光束干涉，所以在许多方面都类似于法布里-泊罗光具座。显然，入射在衍射光栅上的每种波长的光波都会产生自身的衍射图。利用这种原理可以分析入射光的光谱，也可以选择和测量特定成分的波长。用分辨率参数最容易表明其完成这些任务的能力，其定义与法布里-泊罗光具座一样：

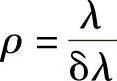
式中，δλ为最小可分辨的波长差。如果λ代表下述情况下的波长差，即p级λ+dλ产生的衍射极大值正好落在相同级λ的第一极小值上，那么就有如下关系：

pNλ+λ=pN（λ+δλ）

因此

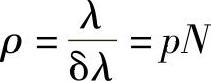
将光栅刻制是，在玻璃（透射）或反射镜（反射）上，在约150mm的长度上，加工出约10⁵条“线”（狭缝）。因此，它的第一级分辨率约为10⁵，比法布里-泊罗光具座的分辨率低一个数量级。然而，这种光栅在制造和使用方面对光学和机械公差要求较低，也比较便宜，并且性能不易随时间恶化。