干涉仪-光子学设计基础

在本书2.7节，已经讨论过双光束干涉的内容，尽管概念上非常简单，但实践中特别有用。其原因在于，干涉条纹的最大值出现在相干光束的相位差为2π整倍数的位置。若一束光束的相位在很小的扰动下就会造成条纹位置有一个横向移动，那么利用这种技术可以很容易观察到大约10^-4的条纹间隔。例如，将一束光束的光路长度增加百分之一个波长，或者（对于可见光）约造成5×10^-9m的位移。这就意味着，可以测量出这种数量级的微小距离。这样就导致非常有用的应用，例如对机械结构的应力监测。

图2.15所示为另外一个双光束干涉仪的例子，其中双光束是由一个半透半反的电介质反射镜或者镀银反射镜M₁产生的。在分别通过各自的光路后，另外一个此类反射镜M₄将这两者重新组合起来。这种结构布局就是众所周知的马赫-曾德尔（Mach-Zehnder）干涉仪，并广泛用监控两条光路之间的相位差变化。图2.16所示检测光纤的马赫-曾德尔干涉仪。在这种结构中，“反射镜”是两个光纤芯间的光学耦合器。由于光纤芯相当于一个有效的空间滤波器，所以“干涉条纹图”实际上只有一个条纹。显然，光纤端部E发出的光，取决于光束重新汇合在R处时两条光路间的相位关系，在很大程度上也取决于两条光路的传播条件。如果一条光路内的温度、应力或者密度相对于另外一条光路发生了变化，那么光的输出也会发生变化。因此，利用这种关系可以灵敏地测量能够改变光纤相位传播性质的任何一个物理参数。

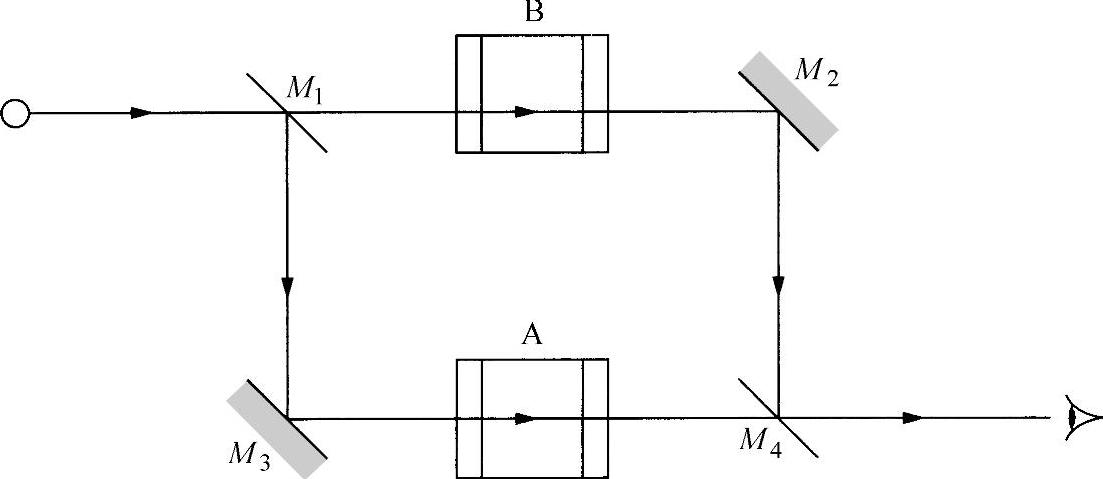
图2.15　基本的马赫-曾德尔干涉仪

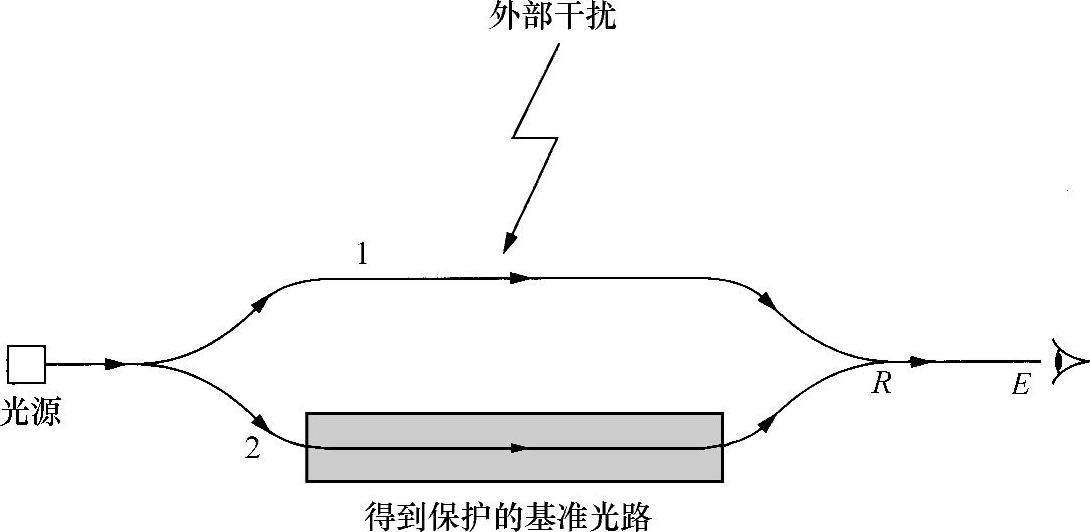
图2.16　光纤型马赫-曾德尔干涉仪

最后，图2.17a表示另外一种更为复杂成熟的改进型麦克尔逊干涉仪。在这种结构布局中，借助于分束反射镜再次将光束分隔开，在两束光路的终端各自放置一个全反射镀银反射镜，使光束重新返回到原来位置。必须使用板P以保证没有任何扰动时两束光具有相等的光路。这种结构布局称为麦克尔逊（Michel-son）干涉仪。它是在19世纪后期，科学家熟练地应用光学干涉法，从而使物理学有了很大发展后实现的。麦克尔逊干涉仪（不要与“测星（stellar）干涉仪”混淆，测星干涉仪将在后面章节介绍）通过控制反射镜能够更为精确地完成精细调整。当然，其基本的干涉原理与前面所述一样，这种装置的光纤型结构如图2.17b所示。

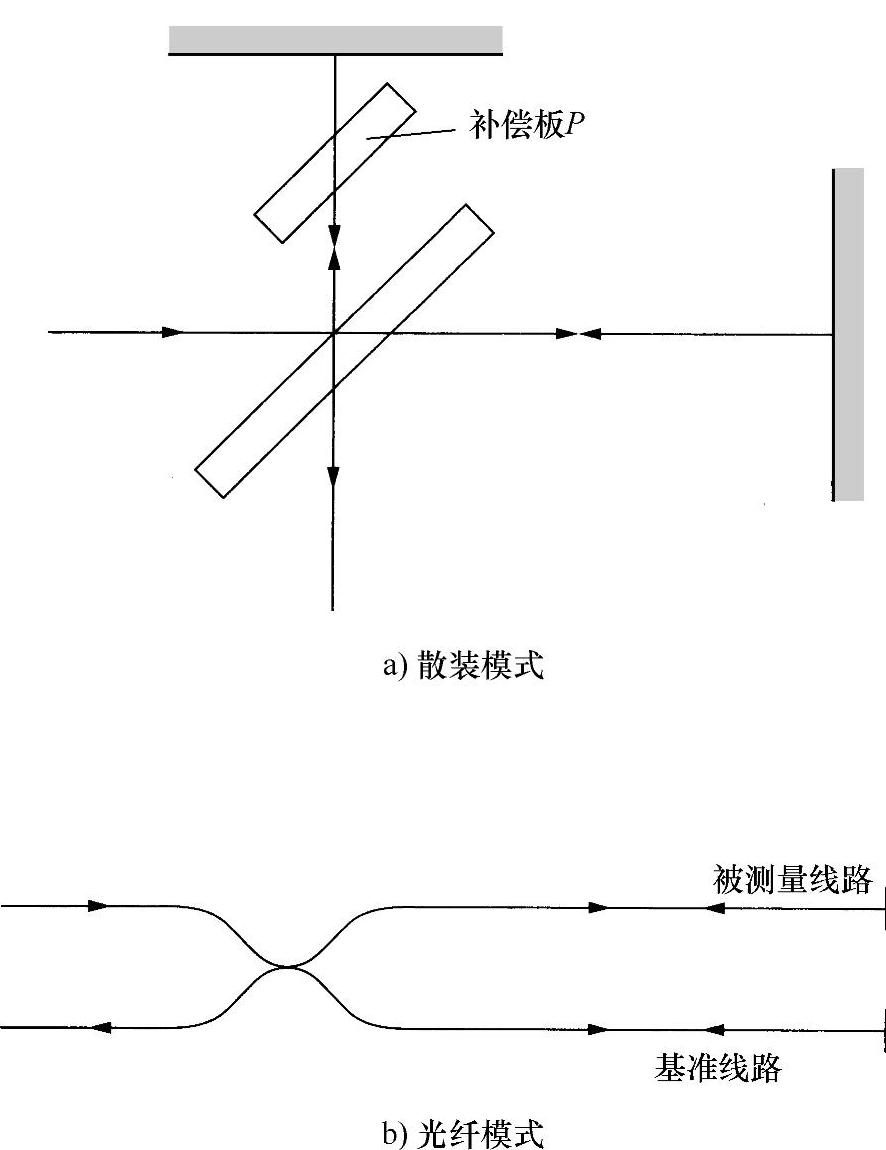
图2.17　麦克尔逊（Michelson）干涉仪

为了保持讨论的完整性，并且由于历史上的重要性，一定会涉及1887年著名的麦克尔逊-莫雷（Michelson-Morley）试验中所使用的麦克尔逊干涉仪。该试验证明了下面原理：无论干涉仪相对于地球在空间的运动是什么方向，光在两条正交光路中都是以相同速度传播。该结果对于爱因斯坦于1905年形成的狭义相对论至关重要，因此无疑也是实验物理历史上最重要的结果之一。

尽管双光束干涉法非常有价值，但有一定局限性，其测量精度取决于正弦变量最大值（或最小值）的位置。对于非常精密的工作，例如精密光谱学，这种局限性是较严重的。使用多光束而非双光束干涉，能够大大提高精度。参考图2.18所示的方案，可以明白这一点。借助于光在电介质板（即玻璃板）内的多次反射和透射，一个点光源发出的光就可以转换成大量的相位相关的不同光束。对于一个给定的入射角θ，会有固定的透射系数T、T′和反射系数R，如图2.18所示。若从振幅为a的一束波开始，在经过连续反射后的波会衰减一定的量，相位也会增加一定的量。如果仅研究透射波，那么能够到达透镜L焦点处的总振幅可以通过求和得到：

A_T=aTT′exp（iωt）+aTT′R²exp（iωt-iks）+aTT′R⁴exp（iωt-2iks）+…

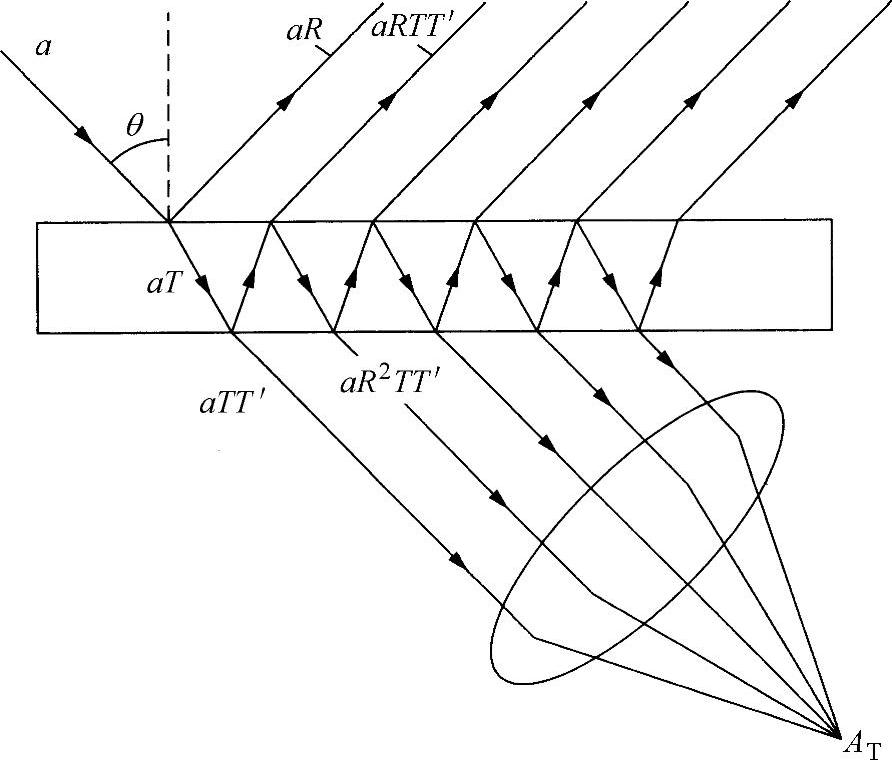
图2.18　多光束干涉

式中，s为在下表面处多次反射之间的光程差（包括反射和透射造成的相位变化）。其和可以表示为

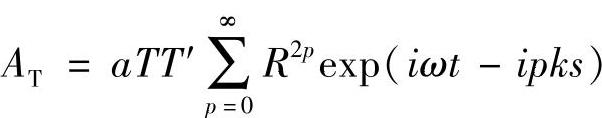
这是一个几何级数，其值等于

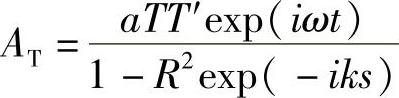
光强度I正比于A²_T，即

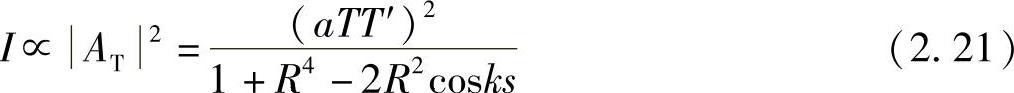
由该式注意到，最大与最小光强度之比为

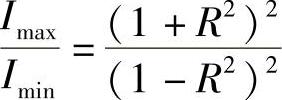
因此，条纹的对比度随R增大而增大。然而，随着R增大，连续反射之间的衰减也增大，因此总的透射光功率将会下降。

图2.19所示为不同R值情况下I随ks的变化。注意到，当R值较大时条纹非常清晰，因此可以精确确定最大值的位置。此外，由于最大值的间隔确定了ks，所以，如果其中一个数据已经知道，就可以利用该数据确定k或s。基于以上分析，可以利用多光束干涉选择（或测量）某种波长，或者测量变化非常小的光路长度。

图2.20所示为从物理学角度解释，为什么随着反射率的增大会使干涉条纹变得越来越清晰：增加多个光波等效于，振幅逐渐在减少而相关相位逐渐在增大的那些矢量相加。若是低反射率（见图2.20a），则该波的振幅快速地减小，因此相位的增大对合成波振幅的影响较小。对于高反射率（见图2.20b），情况正好相反，相位有小的连续变化就会快速减小合成结果。

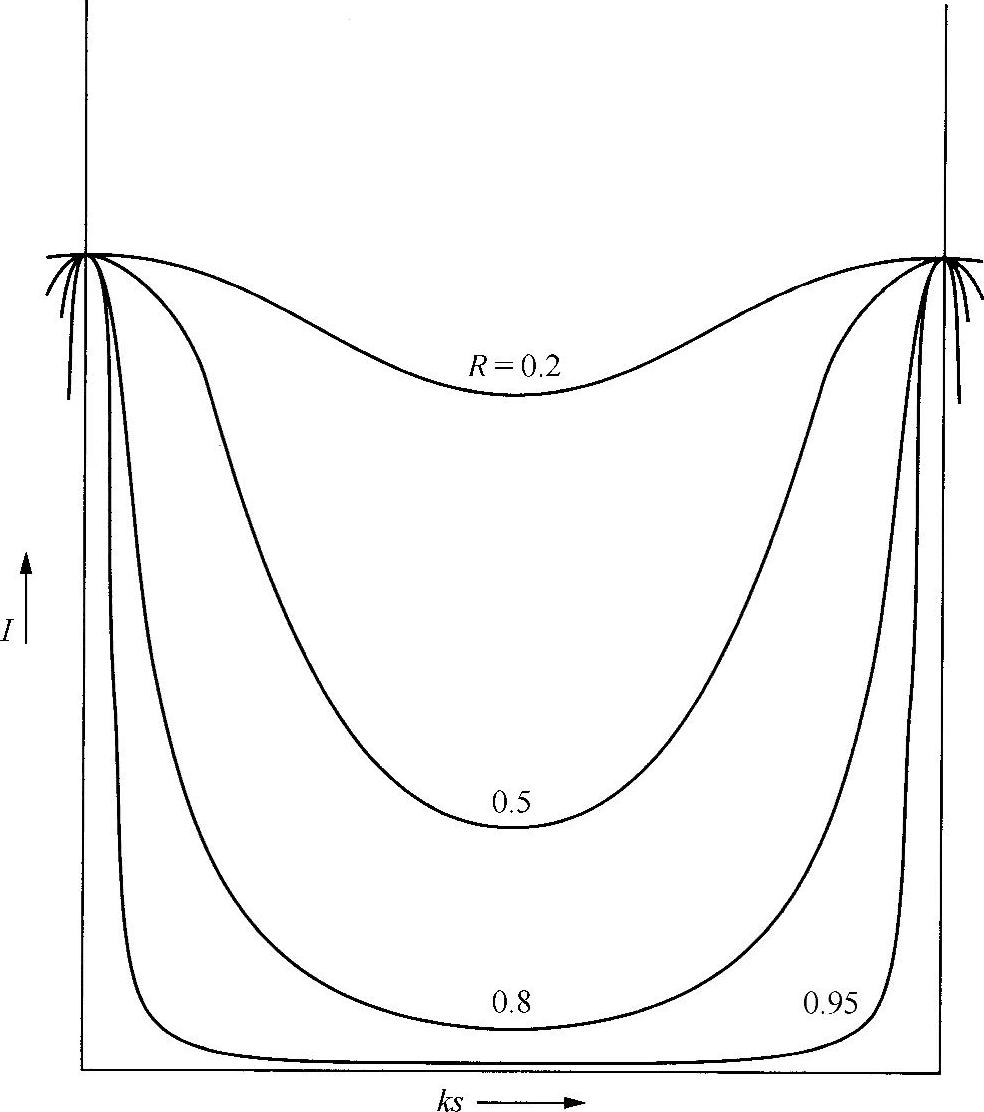
图2.19　多光束干涉板中，不同反射率条件下光强度随光路长度的变化

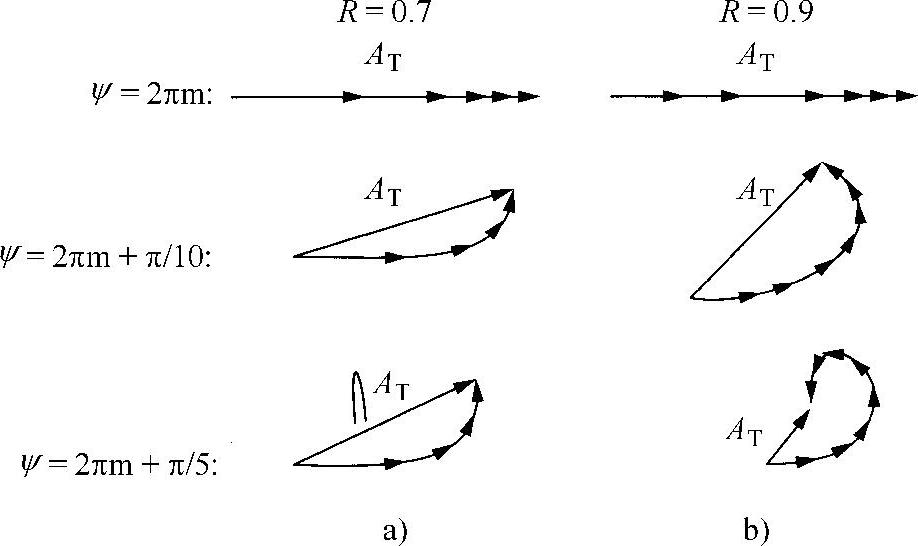
图2.20　条纹清晰度与反射率R的依赖关系

以多次反射原理为基础的两种有非常重要意义的装置是，法布里-泊罗（Fabry-Perot）干涉仪和法布里-泊罗光具座。在法布里-泊罗干涉仪中，为了控制条纹，可以精密微调两个表面之间的距离；而在法布里-泊罗光具座中，两个表面是固定的。在这两种情况中，为了得到高质量的条纹，表面的平面度和平行性必须精确到约λ/100，变间隔装置很难达到这种要求，所以，从实用目的出发，大部分情况下更喜欢采用光具座。

在光子学中，法布里-泊罗干涉仪是特别重要的设备。已经注意到其波长灵敏度，还应当注意，通过使光在两个平行反射镜之间连续不断地反射而使之具有存储光学能量的能力，为此常称之为“法布里-泊罗腔”。粗略地说，在光学上，它类似一个电子振荡器，光学术语是“谐振器”。就是这种性质使其成为所有激光器中必不可少的部件。

由于该干涉仪是如此重要，所以必须更详细地了解表示法布里-泊罗谐振腔性能的有关参数。下面介绍三个主要参数。

正如所期望的，这些参数与仪器能够分开较小间距的密接光学波长的能力有关。第一个参数是条纹清晰度的计量值（即第一个参数为条纹清晰度）。该计量值归化为某种单波长的条纹间隔。很清楚，这样归化的原因在于，如果一些窄条纹都积压在一起，导致不同波长的条纹级相互叠加，这是没有优势可言的。为此，定义一个量：(www.xing528.com)

它称为“条纹间隔宽度比”，大约等效于电子振荡器的Q因子（计量谐振锐度的“质量”因子）。

如下所述，根据式（2.21）很容易推导出Q的表达式。

该式可以写成如下形式：

式中

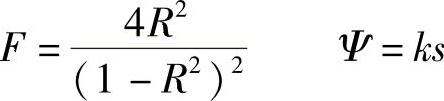
显然，当

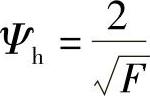
可以得到I=I_max/2

因此，。

两个最大值之间的“Ψ距离”恰好是2π，因此精细度可由下式给出：

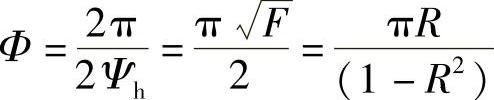
对于双光束干涉仪，该量值为2。对于R=0.9的法布里-泊罗光具座，该值为15。很明显，如果干涉条纹间隔一定，该值越大，条纹越清晰，可供装置选择的波长范围就越大。

需要讨论的下一个参数变量是分辨率，是在某一给定波长λ时最小可探测波长间隔δλ的一种计量值，定义为

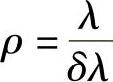
如果令λ对应于一个ψ差（等于半最大值处的宽度），则有：

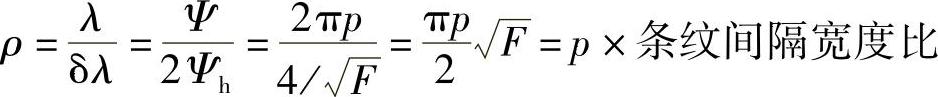
就是说

ρ=pΦ

式中，p为极大值的“序”（Ψ=0时，极值的数目）。若光具座非常接近于正入射，在双通道光具座中，p正好等于波长数目。如果光具座的光学厚度是t，则有p=2t/λ，因此：

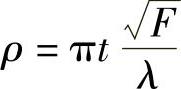
与诸如麦克尔逊双光束干涉仪（“序”的典型值约为10⁴）相比，其“序”的典型值为10⁶。因此，通过这些比值可以看出，利用多光束干涉技术要比双光束干涉仪技术在精度方面的提高程度。

最后，确定有关序的重叠的一个量。如果所研究的波长范围（Δγ）使得γ的（p+1）级极大值与（γ+Δγ）的第p级相重合，显然，会模糊得不可分辨。为此，可以得到：

（p+1）k=p（k+Δk）

因此

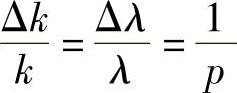
再次重申是正入射，由于p=2t/γ，所以，可以写为

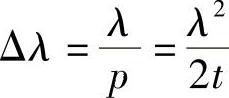
Δγ称为光具座的“自由光谱区”，代表最大的可利用波长范围，与前面给出的会使条纹变模糊的波长间隔无关。

稍后，将专门讨论法布里-泊罗干涉仪。