光的波导及共振条件分析

如果沿Oz方向传播的波是由自然形成的干涉图产生的稳定对称实体，那么波的光强度在两个界面处一定相等，这就要求在x=0和x=2a时是一样的，就是说：

该方程的一般解为

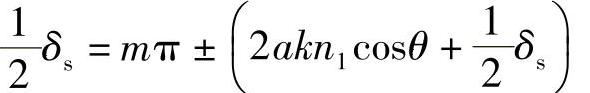
式中，m为任意整数（正或负）。因此，有：

2akn₁cosθ+δ_s=mπ（-） （2.20a）

或

2akn₁cosθ=-mπ（+） （2.20b）

然而，还需要另外的附加条件：如果干涉图按照波导传播方式自动重新形成，那么，一条光线沿波导实现一个完整的“跳动过程”所经历的相位变化一定是2π的整数倍。否则，这些波相位之间不应当具有相干性，并且干涉图自身模糊。图2.14所示的几何图形非常清楚。倘若下面条件成立，光线在波导各点反射所产生的波前只能是同相的：

2akn₁cosθ+δ_s=mπ

图2.14　横向共振条件

该条件对应于式（2.20a）。式（2.20b）不满足波前的条件，所以并不成立。由于式（2.20a）主要对应于下述情况：在求解与波导轴平行和垂直方向的波矢量时，横向分量恰好是1/2个周期，或者mπ的整数倍，与波导宽度一致，所以该公式又称为“横向共振条件”。这就是下述意义下的一种“共振”：拨动两点间的一根绳子，该绳子会以完全相同的方式产生的频率发生共振。(www.xing528.com)

由于δ_s只取决于θ（见2.5节的菲涅尔方程），由此得出结论，下面的条件就是确定θ的条件：

2akn₁cosθ+δ_s=mπ

上式表明，如果干涉图形式上能够在沿光纤长度方向保持不变，θ就只能有某些离散值。所以，各种形式的干涉图都可以用一个具体的m值表示其特性，每个m值对应着一个θ值。容许的干涉图称为波导“模式”，这取决于波导的性质（几何性质和物理性质）。

下面开始讨论波沿波导的传播（沿Oz轴）。可以看出，式（2.18）是由其波数值表示其特性的：

n₁ksinθ=β　（设波数值为β）

此外，TIR条件要求：

得

n₁k≥β≥n₂k

就是说，纵向波数总是位于两种波导介质波数之间。

可以看到，波导基本上是一种波的干涉现象，此处暂时不讨论这项课题。这项课题是一个特别重要的课题，有许多需要研究的内容，因此在本书第8章将较详细地予以讨论。