全内反射及古斯-哈恩森位移

再次从Snell定律开始有：

n₁sinθ_i=n₂sinθ_t

或者

当然，系数sinθ_i总小于1。然而，如果n₂<n₁（即第二种介质的光学密度小于第一种介质（入射光线所在介质）的光学密度），就可能有：

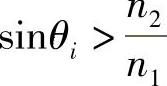
即

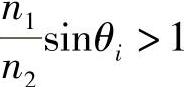
若是这种情况，根据式（2.14）得到：

sinθ_t>1 （2.15）

显然，任何θ_t值都不能满足式（2.15），因而不会存在真正的折射光线。对该现象的解释是，当光从光疏媒质传播到光密媒质时，折射角θ_t总是大于入射角θ_i。因此，在小于θ_i角度情况下，θ_t将达到90°的值（即平行于边界面）；而大于θ_i的任何角度都不可能产生折射光线（见图2.9），满足式（2.15）的θ_i角定义为临界角θ_c，有：

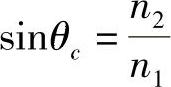
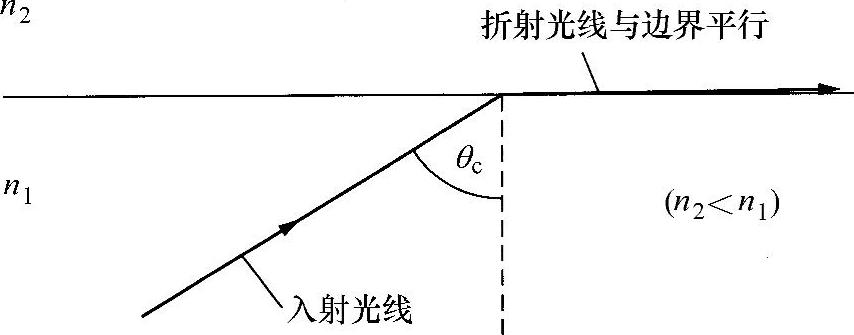
图2.9　全内反射的临界角θc

所有满足θ_i>θ_c的角度值，光在界面处发生全反射，这种现象称为全内反射（Total Internal Reflection，TIR）。然而，还必须应用菲涅尔方程，因为在设置边界条件时没有对这些量值进行约束。此外，如果该场在通过界面时是连续的，正如麦克斯韦方程所要求，在第二种介质中就一定会存在着某种类型的场扰动，可以利用菲涅尔方程讨论这种扰动。

写出下面关系式：

cosθ_t=（1-sin²θ_t）^1/2 （2.16）

当θ_t>θ_c时，sinθ_t>1，并且，对所有实γ值，函数coshγ≥1，所以为了方便，可以进行替换：

sinθ_t=coshγ（θ_i>θ_c）

所以，这意味着自此以后，施加了TIR条件（即式（2.15））。由式（2.16）得到：

cosθ_t=i（cosh²γ-1）^1/2=±isinhγ

可以将第二种介质中的场分量写成下面形式：

exp{iω[t-n₂（xcoshγ-izsinhγ）/c]}(www.xing528.com)

或

exp[（-ωn₂zsinhγ）/c]exp[iω（t-n₂xcoshγ）/c]

式中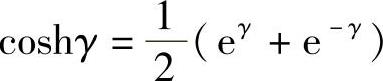，。当γ→±∞时，该值趋于无穷大；在γ=0处有最小值1。

这就代表着在第二种介质内沿Ox方向（平行于介质面）传播的波，其沿Oz方向的（与边界面垂直）振幅按照指数形式下降。振幅随z的下降量可以写为

exp[（-2πzsinhγ）/γ₂]

或者按照初始参数表示为

exp[-k₂z（n²₁sin²θ_i-n²₂）^1/2/n₂]

式中，γ₂为光波在第二种介质中的波长；k₂是波数。这表明，光波在通过距离约γ₂后有很大的衰减。例如，在玻璃/空气界面，临界角是arcsin（1/1.5），即约42°，对于以60°角（θ_i>θ_c）入射到玻璃/空气界面处玻璃内的光波，sinhγ=1.64。因此，仅仅在一个波长范围内，光波在第二种介质中的振幅就会减小一个因子5.4×10^-3的长度，波长是1μm数量级。这种波称为“渐逝波”。即使渐逝波能够在第二种介质中传播，但在垂直于边界面方向上没有光能量传输，所有光在界面处全都发生内反射。存在于第二种介质中的场给出一个坡印廷矢量，在一个光波振荡期内，该方向上的平均值是零。渐逝波的全部能量平行传输到两种介质的界面。全内反射波会有一个相位变化，这取决于入射角和偏振两个因素，用菲涅尔方程式可以很容易推导出。根据式（2.12a），对于E分量位于入射平面内的TIR情况，有如下形式：

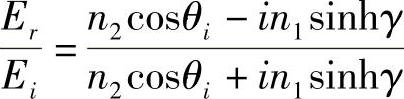
该复数形式将TIR的相位变化定义为δ_p，有：

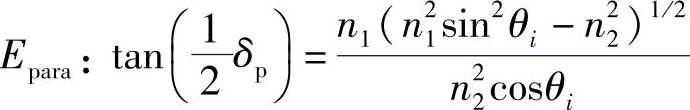
对于垂直的E偏振：

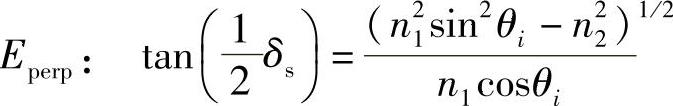
还注意到

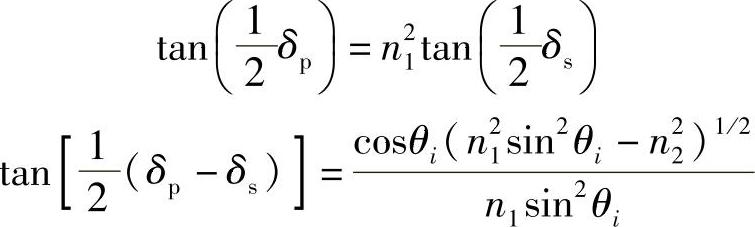
图2.10给出了δ_p、δ_s和δ_p-δ_s随δ_i的变化。显然，发生TIR的光的偏振态变化是δ_p-δ_s差分相位变化的结果。适当选择θ_i，利用两次TIR，有可能从指定的初始态得到所需要的最终偏振态。

图2.10　全内反射造成的相位变化

很高兴注意到，发生TIR时的反射光线似乎源自入射点所在界面上的一个点，就相当于第二个界面内相距非常近的一对平行平面对入射光线的反射（见图2.11）。这种认识与观察到的相移是一致的，可看作是光线传播了额外的光路。这种移位称之为古斯-哈恩森（Goos-Hänchen）作用，并对TIR给出了完全一致的另类解释，为进一步发展新奇的思维提供了资料。由于已经超出了本书的讨论范畴，将不做进一步研究。

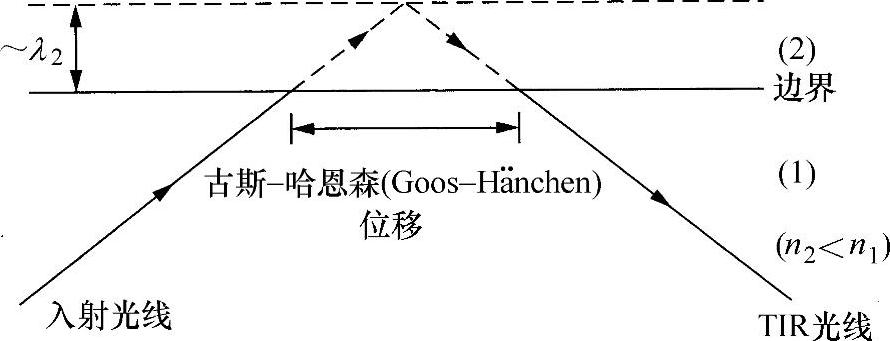
图2.11　关于全内反射的古斯-哈恩森（Goos-Hänchen）位移