光线的反射和折射规律及波动理论解释

在2.4节已经看到，麦克斯韦方程得到一组下面形式的解：

E_x=E₀exp[i（ωt-kz）]

H_y=H₀exp[i（ωt-kz）]

式中，ω/k=（εμ）^-1/2=c。

该公式代表沿Oz方向传播的平面波。现在讨论这类波的特性，要特别关注不同光学介质界面处发生的效应。

当然，也可能会有其他类型的解，一个重要的解就是从一个点呈球面状向距离为r处扩散的波：

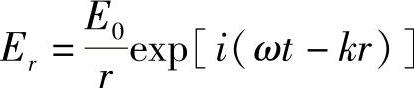
其中，为了保证能量守恒（根据坡印廷矢量），必须在振幅中含有因子1/r；显然，因为能量流通过的总面积是4πr²，所以强度变成1/r²（注意，强度正比于振幅的二次方）。

感兴趣和有意义的是，一束平面波的传播（见图2.4）等效于该平面波传播波前上每一点辐射出的球面波的传播。在一个特定的波前上，每一点处的波开始同相传播（这就是波前的定义），所以，只有在与传播方向垂直的方向（见图2.4），这些波才严格地保持同相。平面波似乎就在该方向传播。惠更斯（Huygens）首先清晰地阐明了这种等效原理，后来由基尔霍夫（Kirchhoff）以数学形式予以证实^[2]。一般来说，在研究波的传播现象时，这是非常有用的。

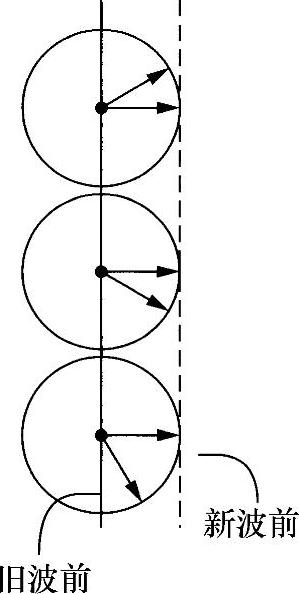
图2.4　惠更斯原理示意图

反射和折射定律首先是根据“光线”的概念推导出的。已经注意到，（约1600年）在处理“点光源”问题时，始终认为光是以下面方式通过孔径：该点发出的光线以直线形式传播（就是这种观点导致牛顿的“微粒子”学说）。让这种实用概念合法化主要基于下面的事实：使这种光通过一个小孔从而可以隔离出一条“光线”，在材料边界处反射和折射的性质就以公式化的形式得以描述：

1）在两种介质边界处的反射　反射光线、入射光线与入射点处边界的法线位于同一平面（入射平面）内，反射角等于入射角。

2）在两种介质边界处的折射　折射光线也位于入射平面内，折射角与入射角的正弦之比是一个常数（Snell定律）。

这两个定律是几何光学或者“光线”光学的基础。大部分宏观光学件（透镜、反射装置和棱镜）的设计都可以借助该定律完成，然而同时也受到了严格限制。例如，在这种情况下不能计算反射光线和折射光线的光强度。

如果企图隔离出一条非常细的光线，而且孔径做得非常小，那么该光线的发散度不会增大而是变小。当孔径变得可以与光波波长相比较时，就会出现这种情况。并且，在这种条件下，几何光学理论不再适用，“衍射”出现了。实质上，这是一种波动现象。波动理论提供一种更为完整，但也更为复杂的光传播理念。现在，利用波动理论解释反射和折射现象。但应当记住，在一定条件下（孔径尺寸必须比波长大），由于简单，所以光线理论是有用的：可以用沿着同相位表面法线传播方向上的一组光线代替一束波，并且遵守几何光学定律。

现在研究折射率为n₁和n₂的两种非导电介质，被一个平面界面隔开，如图2.5所示。该平面表示为z=0处的xy平面。一束平面波位于xz平面内，并在介质1中传播，以角度v_i入射到界面上，如图2.5所示。如图2.6所示，利用2.3节介绍的波的指数表示形式，并指定c是自由空间中的光速，那么所有的场分量，例如（E_i，H_i），都将变为

（E_i，H_i）exp{iω[t-n₁（xsinθ_i+zcosθ_i）/c]}

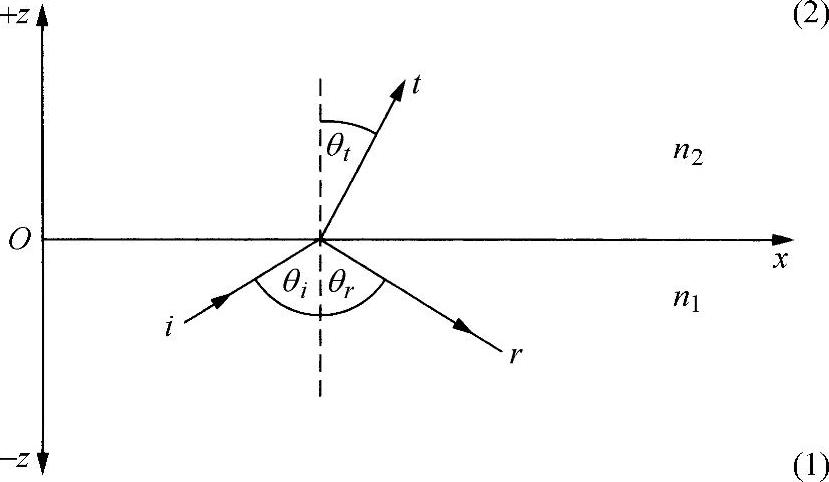
图2.5　两种介质界面处的反射和折射

一般来说，光线入射到界面上，会产生一束反射波和一束折射波（透过波t）。这种现象是边界条件的直接结果，在两种介质的界面处必须满足这些条件。这些条件源自麦克斯韦方程，描述如下：

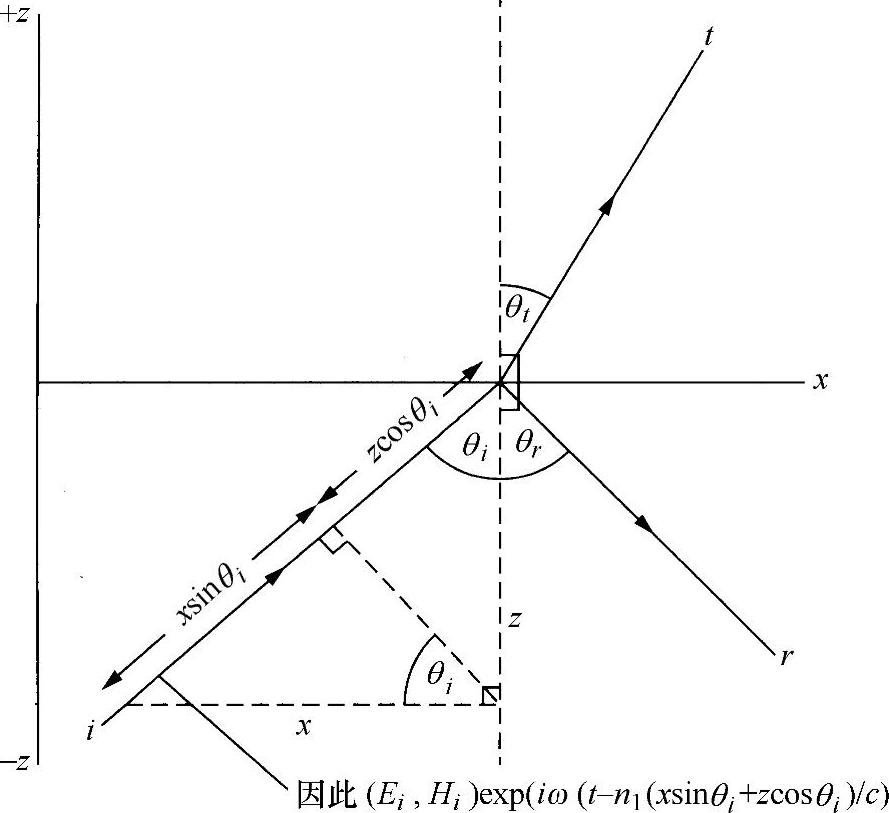
图2.6　入射光线的三角几何示意图

1）E和H的子午分量连续通过界面。

2）B和D的垂直分量连续通过界面。

无论何时及在界面上任何位置，上述条件都是正确的。如果所有波（入射、反射和折射波）的频率一样，那么只有在给定点才是正确的，否则振幅将会不连续地通过界面。此外，由于界面上入射光波的振幅和相位在沿x值不变的一条线上必须是不变量（见图2.7），由此得出结论：如果符合边界条件的连续性保持不变，那么沿这条线的反射波和折射波的相位和振幅是不变的；这就是说，反射波和折射波是在相同的方向上传播，并与入射光线位于同一平面内（xz平面），从而证明了前面论述的反射定律和折射定律中的一个定律。

为了继续讨论，必须对这些波给出合适的数学表达形式。当然，任何一束指定的波都是正弦波，其振幅、频率和相位就可以将该波完全确定下来。2.3节已经指出，表示这种波的最方便方法是复指数形式。

如图2.6所示，假设反射波和折射波分别与xz平面内的边界所形成的角度是θ_r和θ_t，那么，这些波将变为

反射波exp{iω[t-n₁（xsinθ_r-zcosθ_r）/c]}

（注意到，反射光线在z的负方向传播）

折射波exp{iω[t-n₂（xsinθ_t+zcosθ_t）/c]}

为了便于参考，写出入射波的表达方式：

入射波exp{iω[t-n₁（xsinθ_i+zcosθ_i）/c]}

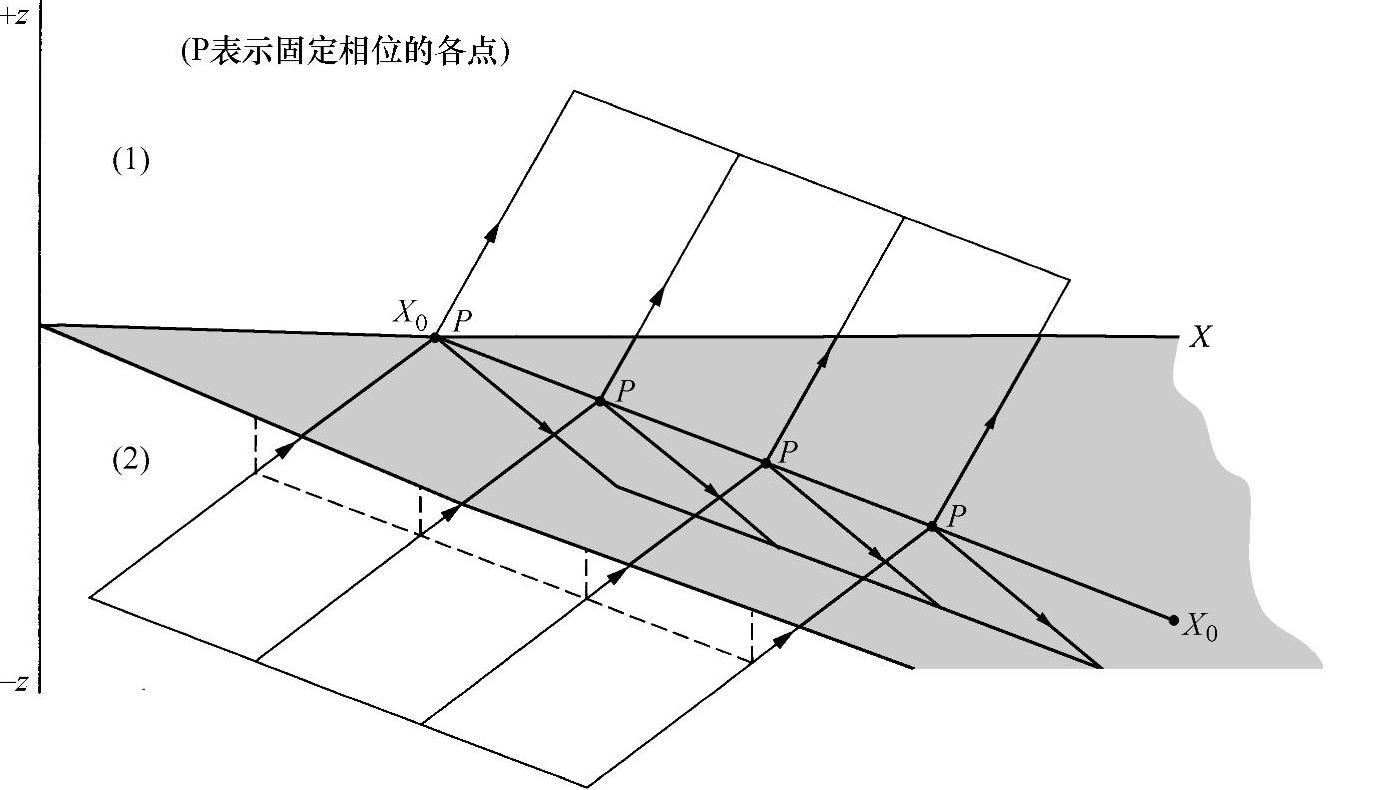
图2.7　边界平面内恒相位线

在边界处（z=0），如果连续性保持不变，那么，对于任意的x和t，这些变量必须相等，因此有：

n₁xsinθ_i=n₁xsinθ_r=n₂xsinθ_t

则

θ_i=θ_r　（反射定律）

n₁sinθ_i=n₂sinθ_t　（Snell折射定律）

现在，必须研究波的相对振幅。为此，分别匹配E、H、D和B的分量。问题的复杂性在于，这些量在边界处的值取决于入射波的E和H场相对于该波平面的振动方向，所以需要分别考虑两个线性正交的偏振分量：一个位于xz平面内，另一个与其垂直（其他偏振态都可以分解成这两个线性分量，从而可以依次完成求解）。

下面依次讨论上述两个分量。

（1）入射平面内的E，H垂直于入射平面

现在，入射波可以写成下面形式（见图2.6）：

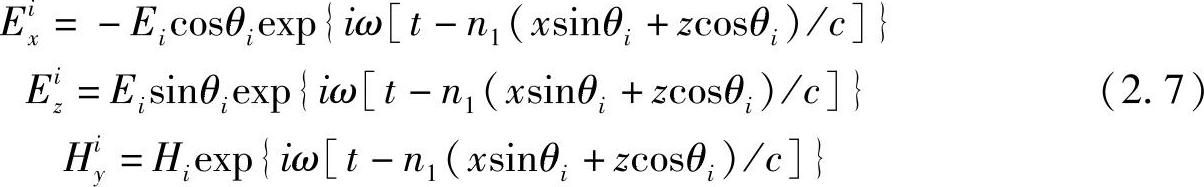
对于一束平面波，再次借助麦克斯韦方程式将H与E联系起来（见本书附录Ⅰ）。有如下形式：

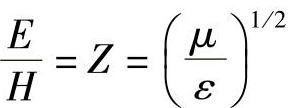
其中，Z是介质的特征阻抗。在该情况下是研究非传导电介质材料，μ=1，n=ε^1/2，因此有：

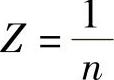
进而

H_i=nE_i （2.8）

则Hⁱ_y的表达式就变为

Hⁱ_y=n₁E_iexp{iω[t-n₁（xsinθ_i+zcosθ_i）/c]}

显然，对于反射波和折射波，可以建立一组类似的方程式，之后附加上边界条件，就可以得到波振幅间的关系。也就是说，在这种情况下，是反射与入射电场振幅间的关系，以及折射与入射电场振幅间的关系。现在就来推导这些关系式。

已经知道，如果能够完全满足边界条件，则边界处的指数因子就都是一样的。所以，可以将通用的指数因子写作F。

对于入射波i，根据式（2.7）有：

如果是反射波r，则有：

对于折射波t，则有：

E^t_x=-E_tcosθ_tF　（原文中等号右侧E_t将错印为是E_r。——译者注）(www.xing528.com)

E^t_z=E_tsinθ_tF（t）

H^t_y=H_tF

加上下述条件，E的子午分量（x分量）在通过边界时必须是连续的，就有：

Eⁱ_x+E^rx=E^t_x

或

-E_icosθ_i+E_rcosθ_r=-E_tcosθ_t （2.9）

适当利用i、r和t的方程式，消除因子F。

同样，完成子午H场（y分量）的运算则有：

H_i+H_r=H_t （2.10）

从式（2.8）还知道：

H_i=n₁E_i，　H_r=n₁E_r，　H_t=n₂E_t

因此，H场的条件，式（2.10）变为

n₁E_i+n₁E_r=n₂E_t （2.11）

现在，由式（2.9）和式（2.11）消除E_t，从而得到（还要记住，θ_r=θ_i）：

这就是所需要的关系式。

根据Snell定律，由于n₁sinθ_i=n₂sinθ_t，所以上式可以写为

同样，根据式（2.9）和式（2.11）消除E_r，并得到：

现在，研究其他正交偏振类型的波。

（2）E垂直于入射平面，H位于入射面内

利用前面的方法，得到下面关系式：

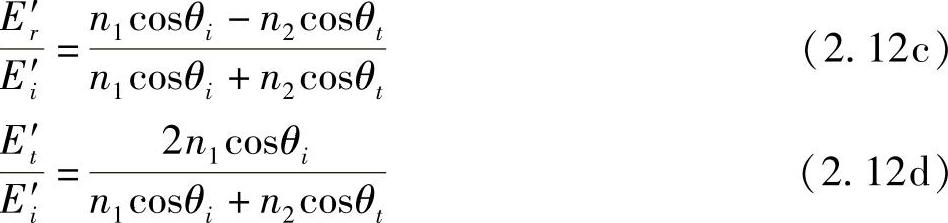
众所周知，式（2.12a～d）上述4个公式是菲涅尔（Fresnel）方程式。Fresnel根据光的弹性固体理论推导出该公式，当时比较成功，并甚为流行。对于这些公式，有几点值得强调说明。

首先注意到，有消除反射波的可能性。如果E位于入射平面内，由式（2.12a）发现，当下式成立时会出现这种情况：

n₁cosθ_t=n₂cosθ_i

根据Snell定律，还有：

n₁sinθ_i=n₂sinθ_t

将两个公式联立：

sin2θ_i=sin2θ_t

该公式有无穷多个解，但只有一个感兴趣的解满足θ_i≠θ_t（只有n₁=n₂才会使θ_i=θ_t），并且，θ_i和θ_t都位于0～π/2范围内。所需要的解为

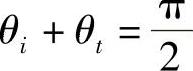
简单的几何图形要求：反射光线和折射光线彼此垂直（见图2.8）。显然，根据Snell定律，下述条件成立时会出现上述这种情况：

n₁sinθ_i=n₂cosθ_i

即

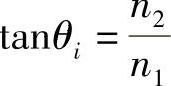
θ_i的具体值称为布儒斯特（Brewster）角（θ_B）。例如，在玻璃-空气界面时，θ_B=56.3°。

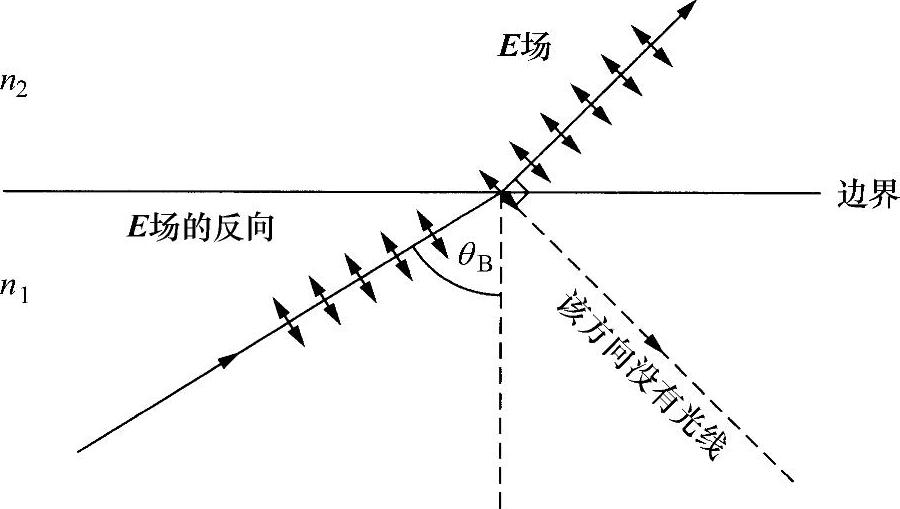
图2.8　在满足布儒斯特（Brewster）角（θ_B）条件下可以清除反射光线

充分了解当电场位于入射平面内，处于布儒斯特角位置的反射光线会消失的物理原因，是非常有益的。如图2.8所示，注意到，入射波使第二种介质中的基本偶极子振荡（详细内容，见本书第4章），在布儒斯特角时，这些振荡发生在反射光线方向，因为折射光线与反射光线是正交的，因此这些振荡不可能在所需要的反射方向产生任何横波。就其本性而言，由于光波是横波，所以一定没有反射波。当E位于入射平面内，若要对偏振提出同样问题，则由式（2.12c）可以得到：

n₁cosθ₁=n₂cosθ₂

利用Snell定律有：

tanθ_i=tanθ_t

该方程式没有解满足所需要的条件，所以在此不可能消除反射波。如果一束偏振波以布儒斯特角入射到边分界面上，只有垂直于入射平面的E分量的偏振发生反射，这是一种非常有用的形成线偏振的方法。

需要强调的第二点是垂直入射状态下的条件。在此情况中，θ_i=θ_r=θ_t=0，因此关系式（对于两种偏振是一样的）变为

波的光强度正比于电场振幅的二次方，但仅对某一指定介质而言。因为从式（2.6c）知道，强度正比于折射率及场的二次方。

因此，由于入射波和反射波在同一介质中传播，所以非常适合写为

若是透射波则为

注意到

I_r+I_t=I_i

所以，正如所需要的，能量是守恒的。

式（2.13c）和式（2.13d）是非常有用的表达式，当光波从一种介质（如空气）透射到另一种介质（如玻璃）时，可以计算出垂直反射会造成多少能量损失。例如，光通过一个玻璃透镜时（空气→玻璃→空气），如果玻璃的折射率为1.5，根据式（2.13c）就可以确定在透镜前表面（假设接近垂直入射）上的能量损失为

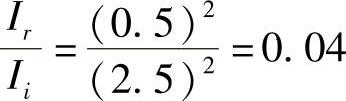
透镜后表面也有4%的损失，总的“菲涅尔（Fresnel）损失”是8%。镀“抗反膜”可以减少这种损失，这是后面章节要讨论的课题（见本书10.2节）。

最后，应当注意，所有表示场振幅值之比的公式在数学上都是实值，因此边界面上的相位变化一定是零或者π。下面研究的现象是另外一种完全不同于此处所述的反射类型。