光学偏振现象及特性讨论

现在，简要介绍什么是光波偏振（该主题将在本书第3章全面讨论）。

当然，由式（2.1）得到的麦克斯韦波方程式的典型正弦解只是无穷多个该类正弦解中的一个，角频率为ω的正弦曲线的一般解为

E（r，t）=E（r）exp（iωt）

一般来说，式中，E（r，t）、E（r）为复矢量；r为xy平面内一个实的半径矢量。

为了简单化，如果只讨论平面单色（单频率）波在自由空间中沿Oz方向传播，对于电场E，就可以写出波方程式的一般解形式：

E_x=e_xcos（ωt-kz+δ_x）

E_y=e_ycos（ωt-kz+δ_y）

式中，δ_x、δ_y为任意的相位角。可以用两种波完整地描述这个解：一个是完全位于xz平面内的电场，另一个则是完全位于yz平面内的电场（见图2.3）。如果在z方向的某特定位置，即z′处观察这些波，则有如下的振动方式：

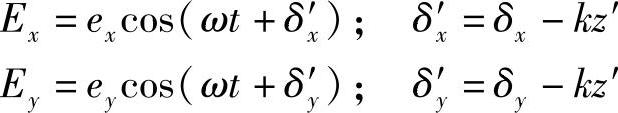(www.xing528.com)

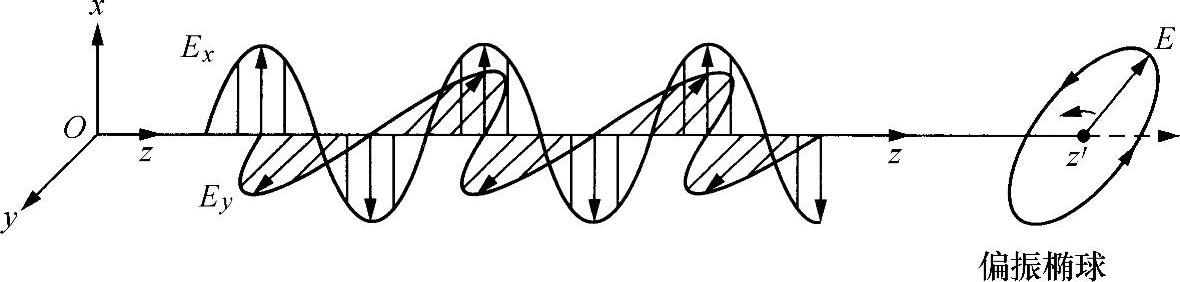
图2.3　一个椭圆偏振波的电场分量

每个矢量的端部似乎都按照正弦方式沿着一条线随时间振动，E_x在Ox方向是线偏振，E_y则在Oy方向是线偏振。

一般来说，E_x与E_y之和形成的矢量端部描述的是一个椭圆，在特定的z′位置处的xy平面内，通过消除E_x和E_y表达式中的ωt，就可以得到其笛卡儿坐标系方程式：

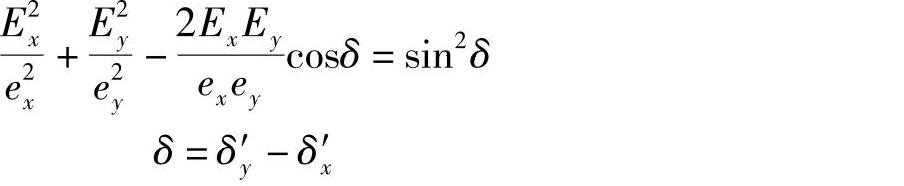
如果（a）e_x≠0，e_y=0；或者（b）e_x=0，e_y≠0；或者（c）δ=mπ，其中m是正或负的整数，则该椭圆就变成一条直线。这与下述条件相对应：E_x和E_y同相或者反相。

如果（a）e_x=e_y和（b）δ=（2m+1）π/2，即这些波振幅相等、相位正交，该椭圆就变成一个圆（该光就是圆偏振光）。

对于在各向异性介质中传播的光，其物理性质随方向变化，所以光波的偏振性质尤为重要。一般来说，在这种情况下，E_x分量的传播性质不同于E_y分量的性质，e₁、e₂和δ值沿传播光路也是变化的。光波的偏振状态与传播距离和介质状态没有关系，这些内容将在本书第3章详细讨论。