能量、功率和强度简介

现在讨论波的能量问题。对于电场，单位体积内的能量u_E由下式给出（见参考文献[1]）：

若是磁场，则有：

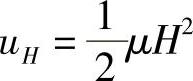
根据下面公式（见本书附录Ⅰ），Maxwell方程将一束电磁波的E和H联系在一起：

因此，波的总能量密度为

u=u_E+u_H=εE²=μH² （2.5）

现在讨论沿Oz方向（见图2.2）传播的平面波。在Oz方向单位时间单位面积上通过的总能量就是包含在立方厘米体积内的能量，其中c是波速。因此，单位面积上的功率通量为

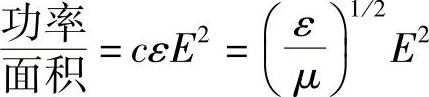
显然，如果电场E按照正弦方式变化，则该量也按照正弦方式变化。举例来说，如果：

E=E₀cosωt

（原文漏印了上面两个公式。——译者注）

该量在一个振动周期内的平均值就称为波的“强度”（有时称为辐照度）；对于不能对光学频率有所响应的器件和装置（适用于绝大多数情况），可以清楚表示单位面积上的可测量功率。

因为cos2ωt平均值为零，因此有：

式中，<>表示平均值。(www.xing528.com)

显然，I与电场振幅的二次方成正比，由式（2.5），也与磁场振幅的二次方成正比。I的米千克秒制（MKS）单位为W/m²。一般地，它可是根据坡印廷矢量Π表示（见本书附录Ⅰ）：

Π=E×H

式中，E和H为矢量；E×H是矢量积（见本书附录Ⅰ和第1章）。波的强度是波在一段时间内Π的平均值。如果E和H在空间上呈正交，并且同相，就如同波在一种各向同性的电介质中传播一样：

I=<Π>=cεE²=cμH²

与前面介绍的一样。正如所期望的，在一些较特殊的情况中（即各向异性介质中），E和H的分量既不正交，也不同相，但<Π>仍然能给出单位面积上的平均功率流。例如，若E和H偶然处于相位正交状态，则有：

I=<Π>=<E₀cosωtH₀sinωt>=0

因此，没有平均功率流（对后面要讨论的“渐逝波”情况，应当注意到这种结果）。

对于μ_R≈1的光学介质，式（2.6a）可以写为

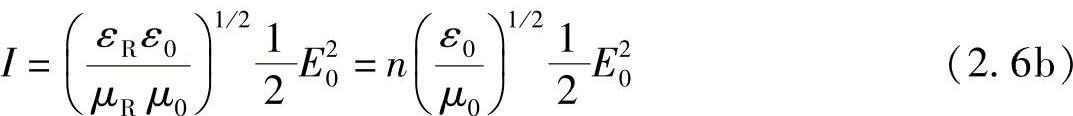
式中，n为介质的折射率。

有时，将（μ₀/ε₀）1/2称为“自由空间的阻抗”，并用符号Z₀表示。这是因为在自由空间有：

由于E的量纲是V/m，H的量纲是A/m，所以Z₀的量纲是Ω（阻抗）。Z₀是实数，用MKS制表示为

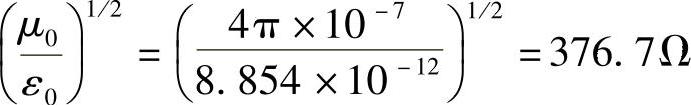
因此断定，式（2.6b）可以写为

这是一个很有用的公式。首先，将一个可以直接测量的量I与不能直接测量的量E₀联系在一起；其次，在I与E₀之间提供了一个确切的数值关系，并且，正如后面所阐述，在设计器件和系统时很有价值。