光子学设计：速度和折射率

1864年，克拉克·麦克斯韦（Clerk Maxwell）最后得出的结论表明，光波实际上是电磁波，并推导出波动方程式，这就是后来众所周知的电磁学定律（见附录Ⅰ）。该波动方程式可以获得与电磁波中光速实验值对应的自由空间内的解。之后，将光波看作是一种电磁现象，是认识过程中一个最重要的进步。

光波的所有重要性质都是通过对Maxwell方程的详尽考查得出的。选取笛卡儿轴Ox、Oy和Oz（见图2.2），利用下面公式可以得到一个有代表性的正弦形式的解：

E_x=E₀exp[i（ωt-kz）]

H_y=H₀exp[i（ωt-kz）] （2.1）

该式表明，电场在xz平面内以正弦形式振动；磁场在yz平面内（即垂直于电场E）振动，并与电场E同相；光波在Oz方向传播。该光波的频率和波长由下式给出：

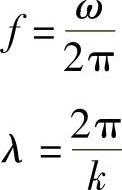
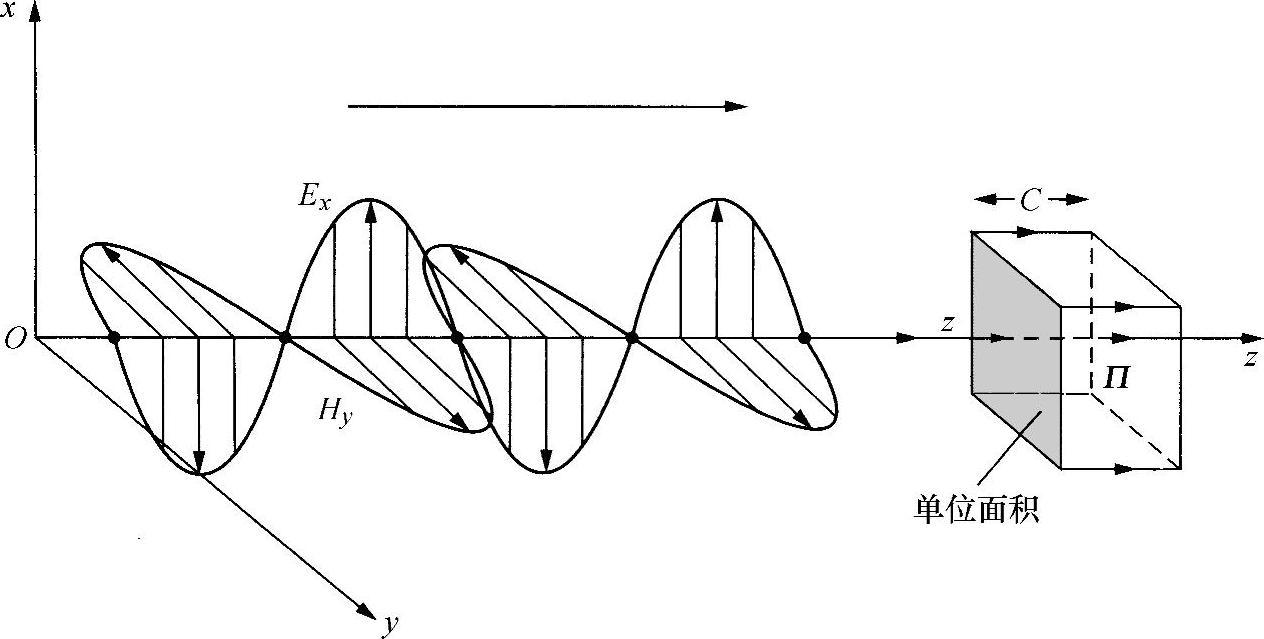
图2.2　电磁波和能量流（坡印延矢量Π）

则 fλ=ω/k=c

式中，c为波的速度。后来，通过下面公式将速度与波传播所在介质的电磁性质相联系，有：

c=（εμ）^-1/2 （2.2）

式中，ε为介质的电容率；μ为磁导率。式（2.2）也可以写成下面形式：

c=（ε_Rε₀μ_Rμ₀）^-1/2

即(www.xing528.com)

ε=ε_Rε₀，μ=μ_Rμ₀

式中，ε_R、μ_R分别为介质的电容率和磁导率；ε₀和μ₀为自由空间中的电容率和磁导率。通常，ε_R称为介电常数。由下面公式确定电位移D和磁通量密度B：

D=εE

B=μH

（出于对称方面的考虑，有时D称为电通量密度）所以，也可以写为

式中，c₀为电磁波在自由空间中的速度，实验值是2.997925×10⁸m/s。

对于有重要应用的大部分光学介质，μ_R≈1和ε_R>1。这些材料属于电介质类材料，是绝缘体，因此可以将式（2.3）写为

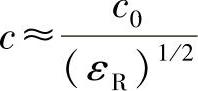
并注意到，c<c₀。根据定义，c₀/c是介质的折射率n，所以有：

n≈ε^1/2_R （2.4）

因此，式中n表示光在光学介质中的传播速度比在自由空间中慢的一个因子。现在，ε_R表示在外部电场作用下介质通过电的方式是否容易偏振化的一种量度（更为详细的解释，见本书4.2节）。这种偏振取决于分子内的电子面对分子力抵制时的迁移率或活动性。很清楚，ε_R依赖于施加电场的频率，因为这取决于这些力能够以多快的速度响应该电场。因此，只有当n和ε_R同属于相同的波频率时，式（2.4）才是正确的。另外，还注意到，n与频率有关。