光子学设计基础：光学波的表现形式

在本章研究光学波的过程中，将定量阐述不同波之间，以及与其他物理实体之间的许多相互关系，这些波都是正弦波形式，有：

E=e₀cos（ωt+φ）（根据傅里叶（Fourier）理论，任何物理场的扰动都可以表示成该正弦形式之和。）

在这些量的运算过程中遇到的一个具体问题是，三角展开式相当麻烦。在这种情况下，即

E₀=e₀cosωtcosφ-e₀sinωtsinφ

例如，如果增加两个具有相同频率的此类波而形成一个合成波，即会形成另外一种具有相同频率的波，但具有不同振幅和相位。在该情况中，研究的目的是确定这种合成波，就是：

e₁cos（ωt+φ₁）+e₂cos（ωt+φ₂）=e_Tcos（ωt+φ_T）

其中的e_T和φ_T代表何意（见图2.1）呢？

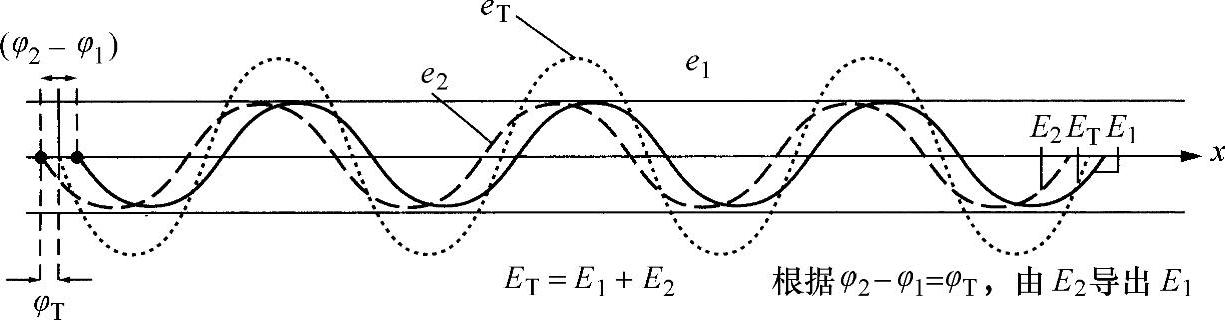
图2.1　具有相同频率的两个波的相加

尽管这种数学表示法很直接，但太冗长、麻烦，容易产生误差，并且随着波的数量增加会遇到更大麻烦。

一个很方便的解是用复指数形式表示正弦函数，从而可以进行因数分解，使数学运算大大简化。由于本书和其他资料都普遍使用该方法，所以花费一些时间进行全面阐述是值得的。

下面形式的正弦波：

E=e₀cos（ωt+φ）

是下列复数表达形式的实部：

E′=e₀cos（ωt+φ）+ie₀sin（ωt+φ）

（由于i[-1的二次方根]完全可以当作一个运算符，作用相当于旋转π/2，因此将正弦和余弦组合，当然是π/2的异相，所以E′可以是一个方便的数学实体。）

现在，众所周知的正弦和余弦的指数表达式为

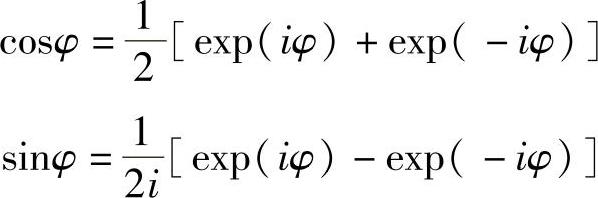
因此

cosφ+isinφ=exp（iφ）

所以

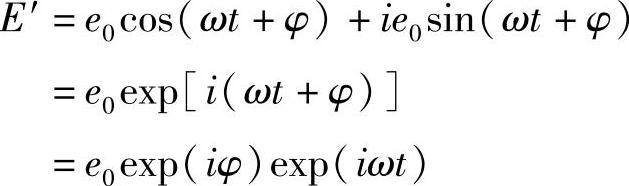
原来的波e₀cos（ωt+φ）恰好是表达式的实部，有时也表示成下面形式：

e₀cos（ωt+φ）=Re[e₀exp（iφ）exp（iωt）]

任何一种正弦形式的波，即使是真正的正弦波（与余弦波相反）都可以写成这种形式，因为在这种情况中必须做的事情就是从相位中减去π/2，即

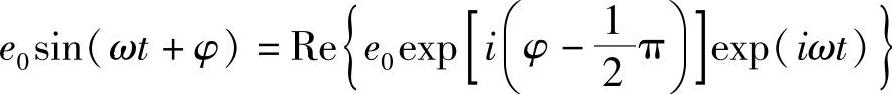
使用这种表达式的真正重要之处在于，如果涉及一组具有相同频率的波，就可以将频率项提出作为公因子，留下一个复数项，其总模数代表波的振幅，总幅角代表波的相位。此处讨论的是一种简单情况，所以有：

E′=e₀exp（iφ）exp（iωt）=Eexp（ωt）

其中

∣E∣=e₀exp（iφ）(www.xing528.com)

并且，E是一个复数，具有下面性质：

E=e₀，arg（E）=φ

同样，对于两个具有相同频率的波，有：

E₁=e₁cos（ωt+φ₁）

E₂=e₂cos（ωt+φ₂）

复指数形式为

E′₁=e₁exp（iφ₁）exp（iωt）

E′₂=e₂exp（iφ₂）exp（iωt）

正如前面那样，假设，期望确定两个波之和产生的波的振幅和相位，可以写成如下形式：

E′_T=E′₁+E′₂=exp（iωt）[e₁exp（iφ₁）+e₂exp（iφ₂）]=exp（iωt）（E₁+E₂）

把复振幅项写作如下形式：

E₁+E₂=a+ib

式中，a和b为实数。因此，合成波的振幅为

e_T=∣a+ib∣=（a²+b²）^1/2

相位为

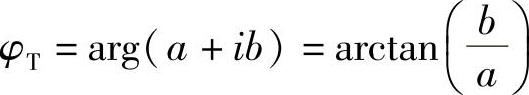
最后得到

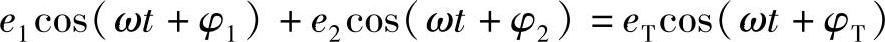
因此

e₁exp（iφ₁）+e₂exp（iφ₂）=e_Texp（iφ_T）

所以

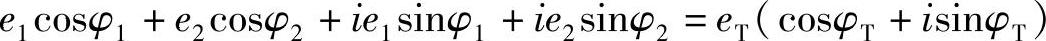
如果使

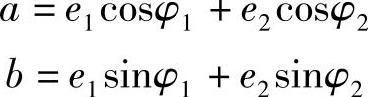
则

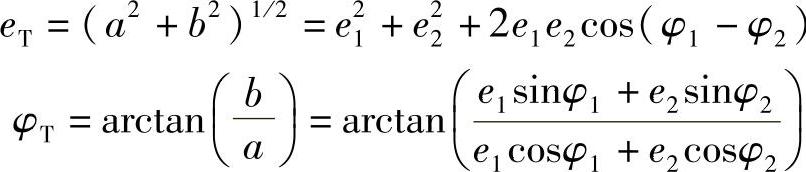
至此，问题得以解决。

与包含余弦展开式的三角恒等式处理技术相比，该方法是一种非常方便的数学运算技术，并且随着波数增加，这种方便变得更加明显。

基于以上原因，本章将全部使用复指数表达式。然而，有时转换成真正的正弦形式也是较为方便的，通常是在光学频率显得极为重要的情况下。以致如果将它作为可分离的复数量公因子消除掉，就不可能非常方便地表述实际的物理条件。