电子的特性及波动性对光子的理解

本书讨论的主题是光子，至此已经专门讨论的内容只是其特性的一半——光学性。这一主题的重要性，源自光子与电子间的强劲反应。显然，同样应当熟悉电子的性质，才能对光子具有全面了解。现在，就来介绍电子的一般特性。

自由电子是一种带负电荷e的基本粒子，电荷量等于1.602×10^-19C，质量m为9.11×10^-31kg。

所有电荷都会对其他电荷施加作用力。对任何一个电荷q，根据电场作用在q上的力F_E，由电场E就可以很方便地确定其他所有电荷的作用：

F_E=qE

磁场不会对一个静态电荷施加作用力，然而，当电荷以速度ν相对于磁感应强度为B的磁场运动时，作用在电荷上的力为

F_B=q（ν×B）

式中，ν×B为ν与B的矢量积，力与ν和B两个矢量都成正交。当然，一个匀速运动的电荷会形成电流，所以，ν×B也表示磁场施加在一个载流导体上的力。洛伦兹（Lorentz）公式将这两种力组合在一起：

F=q（E+ν×B） （1.9）

这也是对自由空间中电子特性的经典描述。对于那些可以将电子看作点质量粒子的应用（如CRT电视中的阴极射线管）中，应用众所周知的电磁力设计电子束装置是足够的。

如果将一个电子（或其他电荷）加速，会产生随时间变化的电流。由于不变电流产生不变磁场，所以一个变化的电流会产生变化的磁场。正如所看到的，这样依次会产生电场，因此有望让一个加速电子辐射产生电磁场。例如，在偶极天线（见图1.5）中，使电子沿传导棒按照正弦方式振动，正弦振动产生加速运动，天线发射无线电波。

电子也呈现波动性。对于一个动量为p的电子，由下式得到相关波长：

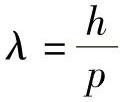
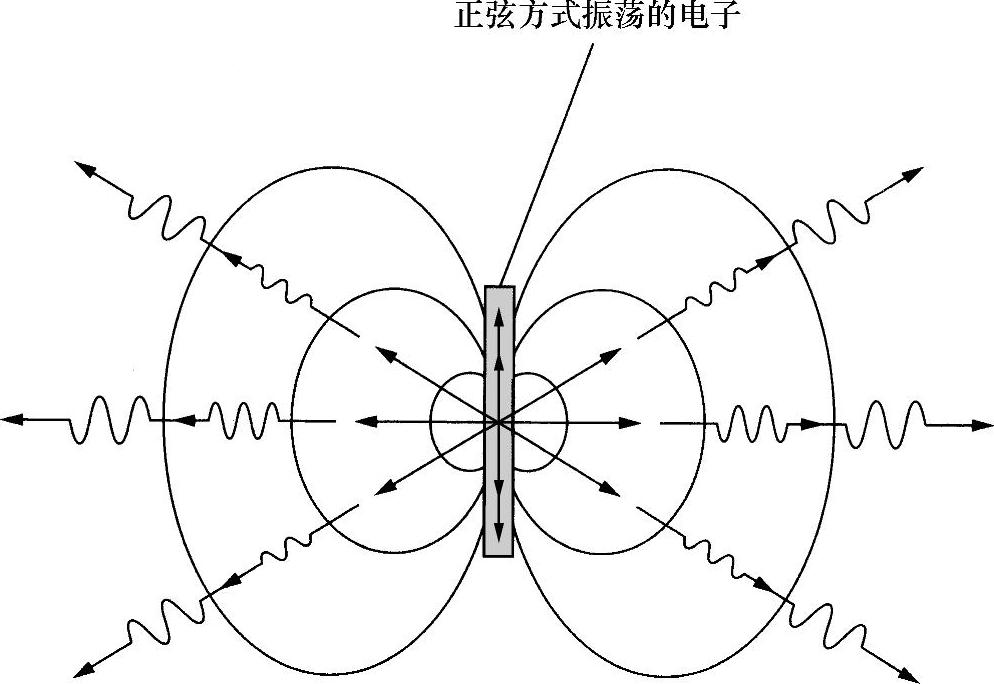
图1.5　偶极发射天线

1924年，弗伦奇曼（Frenchman）提出材料粒子可能呈现波动性（1927年，该提议通过实验得到证实）。之后，该波长被称为布罗格利（Broglie）波长。其中，h是量子常数。

确定电子波动性的重要意义与光子波动性一样：波的强度（正比于振幅的二次方）是单位体积空间内电子概率的一种量度。该波是一种“概率”波，因此，对于电子和光子，粒子波的双重性质具有理想的均衡性。对于这两种实体，其双重性产生的一个直接结果就是不确定性原理：认为无论是电子还是光子，要同时确切理解动量和位置基本上是不可能的。通过下面表达式，不确定性原理将动量Δp与位置Δx两者的不确定性联系在一起：

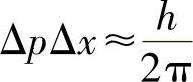
一个系统的能量（ΔE）与能量测量过程中所耗费的时间长度（Δt）不确定性间也有一个对应关系：

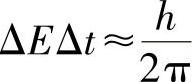
波形图中的解释是，动量的不确定性与波长的不确定性有关——也就是说：

h

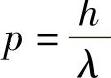
所以

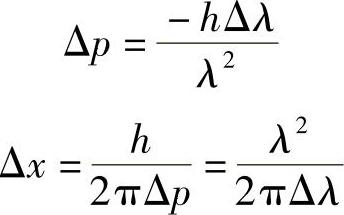
因此，一个粒子产生的波长范围越小，其位置（Δx）的不确定性就越大。换句话说，与粒子相关的波函数越近似于一个纯正弦波，在所有的空间范围内都有固定的振幅和相位，则所知道的动量就越大：如果能够完全精确地知道动量，粒子就会相当好地位于宇宙中的任何位置。

电子的波动性在原子物理学中有许多重要结论。例如，绕核转动的在轨核电子只能占据那些圆周上可以存在恰当波数的轨道，根据波通过势垒会产生“隧道效应”的理论，可以很容易地解释β放射现象中电子从原子核中逃逸的问题。但是，按照目前讨论的观点，这些波动性质中最重要的结论很可能是：固体物质中不呈现电子的特性。而光子学关心的绝大部分问题是固态材料中光子与电子间的相互作用，所以，对这一点我们要更加注意。

与物质的其他形态（气体、液体和离子）相比，固体物质具有的主要特性是：由于其电子概率波相互重叠，固态物质的原子或分子彼此间非常靠近，恰恰就是这种叠加，为形成一种固体材料提供了所必需的原子耦合强度，防止了变形。

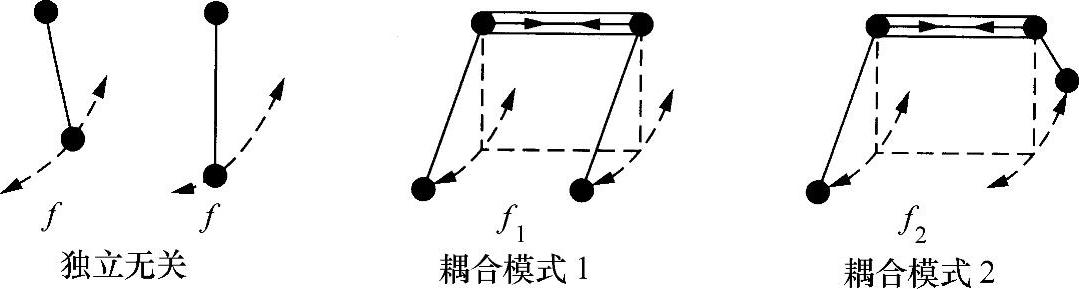
当两个相同的具有特定能级的原子足够靠近，以致其电子波函数（即其概率波）重叠时，其结果是产生一个新的能级组合，有些比原始值低，有些会比原始值高（见图1.6）。其原因类似于两个机械谐振系统，例如两个相同的钟摆所发生的情况：在一个公共支撑杆上摆动，从而产生相互作用（见图1.7）；如果使一个钟摆摆动，它将使另外一个钟摆运动；最后，当第一个钟摆（原文错印为第二个钟摆——译者注）已经静止，而第二个钟摆会以最大振幅摆动，然后该过程逆向进行，返回到原始状态，并以频率f_B重复整个过程。事实上，该系统具有两种与时间无关的固有振荡模式：其一是两个钟摆以相同的振幅、同相摆动，其二是具有相同的振幅反相摆动。如果这两种频率分别是f₁和f₂，则有：

f₁-f₂=f_B

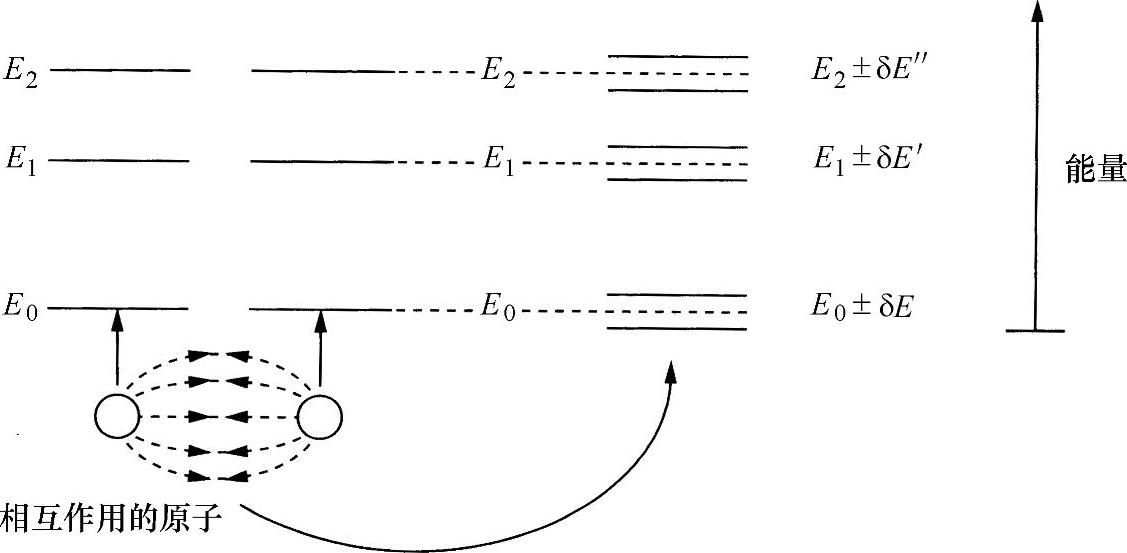
图1.6　两个相互作用的原子造成能量级的分裂

(www.xing528.com)

图1.7　相互作用的钟摆

若彼此无关，则通过下式可以将每一个钟摆的频率f与其联系在一起：

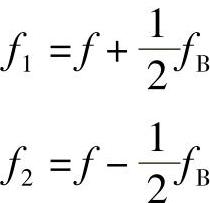
也就是说，在两种频率，即一种较高（f₁）和另一种较低（f₂）频率，相互作用的条件下，原始的自然频率就会被替代。

很容易将这种思想扩展到原子方面，并且可以这样理解：如果包含了大量的原子，一个具体的能量级就变成能级紧密相邻的能量结合带，因此，在一个固体中，可能有希望找到被能隙分隔开的能带，而不是被其隔开的分立级，的确就是这样的。

固体的能带结构可以使人们相当快地定量理解不同类型的固态物质（例如绝缘体、导体和半导体）之间的差别，对总结和概括这些思想是非常有用的。

从基本的原子物理学知识知道，原子中的电子会填充在上升级的合适能态中，因为不会有两个电子占据同一能态：电子（状态）服从Pauli不相容原理。这就意味着，在温度是绝对零度时，N个电子将会充满N个最低能态（见图1.8a）。当温度高于绝对零度时，原子处于热运动状态，一些电子可能被激励到高能态，接着被衰退，建立一种动态平衡，在N个最低能态之上的能态有一个平均的电子占有级。那么重要之处在于，只有最高态的那些电子可以被激励到更高的能级，因为只有这些最高态才会达到空能态（见图1.8b）。这种现象对于理解固态物质的特性尤为重要。如果不是局限于固体内，电子在特定温度下沿能级分布就是费米-狄拉克（Fermi-Dirac）分布，而不是麦克斯韦-玻耳兹曼（Max-well-Boltzmann）分布，例如会有自由移动的气体分子。

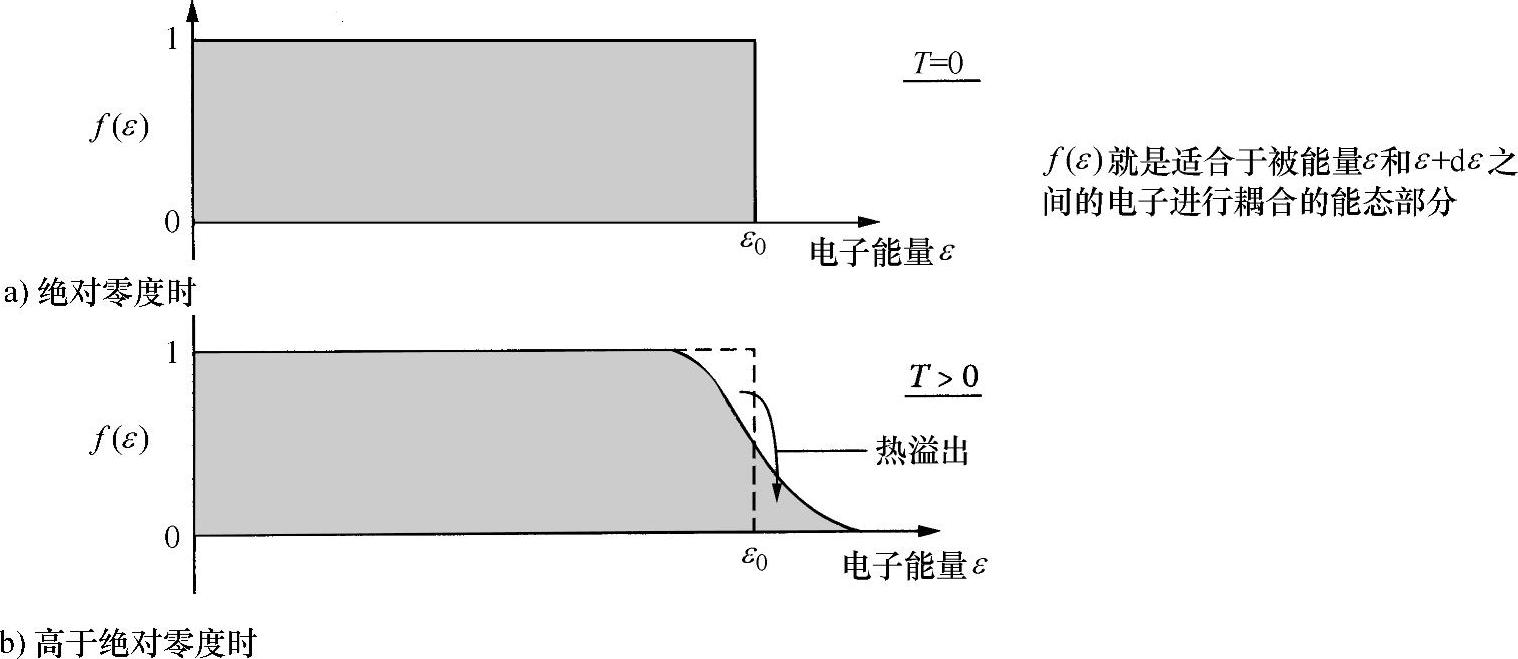
图1.8　固体物质中电子的费米-狄拉克（Fermic-Dirac）分布

现在讨论图1.9a所示的能带结构。电子充满较低能带，在下一个容许空能带接受电子之前有一个大的能隙，因此容许电子得到能量相当困难。如果在该固态物质上施加一个电场，应当说，对电子的影响非常小。原因在于，电子为了移动以适应该电场施加的力，就需要从中得到能量。由于它们不可能越过能隙，所以也不可能获得能量，因此电子不会移动。虽然施加电压，但没有电流输出，这种材料是一种绝缘体。

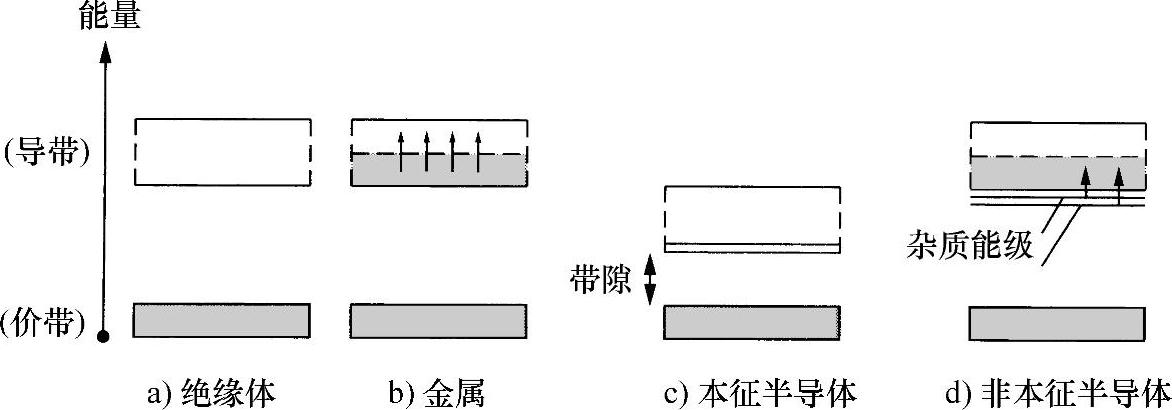
图1.9　三种主要类型的固体材料所具有的能级示意图（T>0）

现在讨论图1.9b所示的情况。最上面的能带仅占有一半电子（该能带上的电子就是原子外层区域中的电子，也就是在原子间产生化学力的电子，即价电子。能保持电子数目不变的最高能带通常称为价电子带），现在的情况完全不同于前面介绍的情况。位于被填充能级最上层附近的电子在易于到达的范围内处于较强的未填充态，很容易从外部媒介，例如施加的电场，得到能量。因此，若有电压，就很容易有电流输出，这种材料是金属导体。

第三种情况（见图1.9c）类似于第一种情况。惟一区别是填充后的价电子带与下一个更高级未满能带间的能隙更小，因此，通过热碰撞可以将比较少量的电子激励到更高阶的能带中（称为传导带）。一旦如此，在施加电场作用下，电子就可以自由运动，这种材料具有低的传导率，称为半导体，更专业地说，是本征半导体（或内禀半导体）。很清楚地，电导率会随温度升高而增大，因为更大能量的热碰撞会将更多的电子激励到导带中。这与金属导体形成鲜明对比，在金属导体中，电导率是随温度升高而减小的（因为较多强烈振动的固定原子之间有较大干涉）。本征半导体有一个更为重要的性质：当一个电子从价带激励到导带中时，会在价带中留下一个未填充态，从而在价带中为那些之前没有机会获得能量，而现在可以通过移动到由第一个电子的跃迁而形成的空态或孔中的电子创造出可移动性。此外，进入孔中的价电子本身又留下了另一个依次可以被填充的孔。所有这些活动的结果是，如果施加一个电场，该孔似乎在与电子相反的方向流动，其特性类似于正电荷（由于缺失了负电荷，这样说就没有什么大惊小怪了）。把电子激励到导带可以看作是创造电子/空穴的过程，每种粒子对施加电压产生的电流都有贡献。

最后，介绍另外一类非常重要的半导体，如图1.9d所示。注意到，在能量“禁”区，即能带隙之间有一些离散的能级，原因是固体材料中含有其他成分，也就是“杂质”。

为了进一步理解该过程，现在研究一种特定固体材料硅。硅原子是四价（即化合价为4）原子，在固态条件下，它们彼此稳定地形成一种对称三维晶格结构（见图1.10）。硅是一种本征半导体，在充满的价带和1.14eV（电子伏）的空（在绝对零度温度下）导带之间存在能隙（1eV是1个电子的势能下降1V所获得的动能，等于1.6×10^-9J）。利用玻耳兹曼关系式，即式（1.6），可以计算出：在室温下，10²⁰个电子中只有1个电子到达导带；但从整体来说，由于材料中每立方厘米有10²⁴数量级的电子数，所以作为半导体的导带这样是足够的。

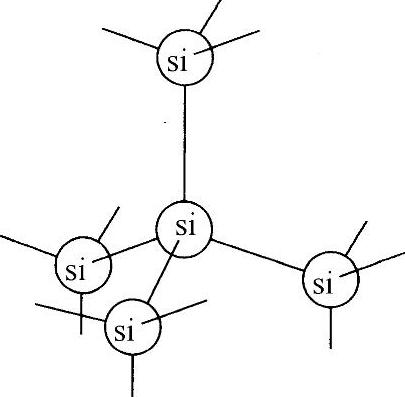
图1.10　硅材料的晶格结构

假设，将某些磷原子注入到硅晶格中，磷是五价原子（化合价为5），所以不能稳定地处于4价（化合价为4）硅结构中。的确发现，在满足晶格要求之后还有一个多余的价电子（与硅有4个价电子不同，磷有5个）。该电子紧密地结合到磷原子上，因此，在小能量的激励下，很容易从其中分离出来而处于一种导带状态。该电子有效地处于与传导带密切结合的状态（见图1.9d），并根据磷原子的密度（即“掺杂”程度），可以产生比纯硅材料大得多的电导率，这种参杂材料称为非本征半导体（或外延半导体、杂质半导体）。

由于在此选择的杂质是将一个电子输送到导带（有一个多余的价电子），贡献的是负电荷载体，所以称为n类半导体。相反，也可以将3价（化合价为3）元素掺杂到硅中，例如硼。在这种情况下，其自身只有3个电子，所以处于额外需要一个电子的状态。结果是，相邻的硅价电子很容易被激励到空位状态，在价电子带有一个正（电荷）穴，该穴增大了电导率，形成p类（正电荷载体）半导体。现在就可以很容易理解（硅中）“5价”元素为“施主”能级，而3价元素为“受主”能级的原因了。

非本征半导体如此重要可以归纳为下面几个原因：首先，通过控制掺杂量来控制电导率的大小；第二，p类材料和n类材料可以进行多种组合，适应不同的装置，形成非常有价值的性质，其中最著名的就是晶体管。现在，千万个晶体管可以集成在一个电子芯片上。

至此，都是按照一般方式理解光子与固体材料中电子的相互作用。

再次讨论本征半导体，例如带-隙能量为E_g的硅。假设一层半导体受到频率为ν的光的照射，且使

hν>E_g

显然，入射光中的单个光子有足够能量将电子从价带提升到导带，在价带中留下正“穴”。现在，如果在半导体上施加一个电压，那么在光照条件下将产生电流（包括移动电子和穴），这样的导体称为光电导体^[1]。此外，只要导带中保留了电子，就会有电流继续流动，并包括从阴极进入半导体片的每一个电子，而与阳极何时吸收电子无关。因此，假如载体的寿命足够长，则电极每秒聚集的电子和空穴数可以大大超过每秒进入半导体片的光子数。如果是硅材料，寿命是几毫秒数量级（取决于载体的密度），电子/光子的增益可以大到10⁴。当然，这也意味着响应时间非常短，因此，光电导体（photoconductor）不能测量光学量级范围内的快速变化（即小于几毫秒的快速变化）。

由于对应的光子能量比较小，所以，必须利用如锑化铟等具有小带-隙性质的材料探测红外辐射。利用窄带隙材料的一个显著困难，是会产生较多的由热激励出的载体，并形成一定程度的噪声。通常，为了获得满意的性能，必须将这些红外探测器致冷，温度至少低于液态氮的温度（即<77K）。

为了提高利用光电导体现象测量光强度参数的速度，可以使用一种由p类和n类半导体材料组合成的器件，即“p-n结”，形成一个“光敏二极管”（见图1.11）。在这种情况中，由入射光子激励出的电子/空穴对在电场中移动通过该结。因此，如前文所述，产生一个可测量的电流。由于电子或者空穴在该结边界处与大量携带相反电荷的载体组合，所以也就各自消失了。减小重新组合的时间会导致反应加快，如果精心设计，可以获得几十个皮秒级的响应时间。除了减少响应时间外，这些p-n结光敏二极管小型紧凑、坚固耐用又便宜，并且可在低压下工作。然而，由于在后面叙述的这些器件无法进行“增益”（不包括本书第7章讨论的雪崩模式中的应用），所以一般不像光电导体器件（photoconductor device）那样灵敏。

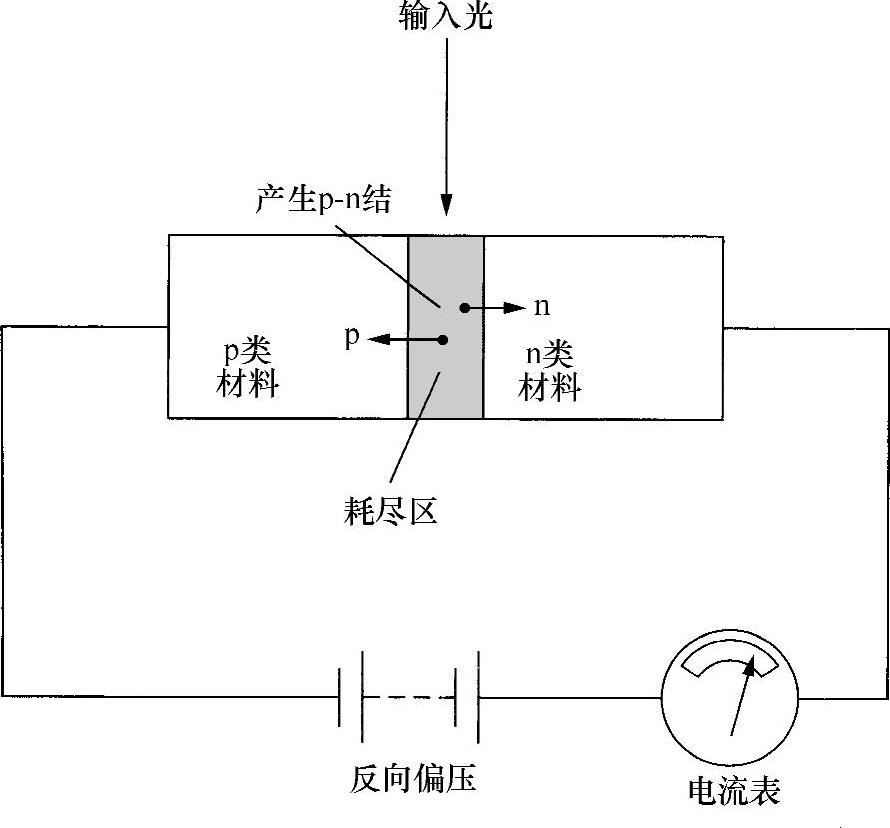
图1.11　p-n结光敏二极管的示意图

也可以以相反方式应用p-n结的检波过程。此时，该器件就变成一个光发装置。在这种应用方式中，是让电流通过器件，利用“正向”偏压将电子注入到p-n结中。电子与p和n材料间跃迁区域内的空穴相结合，并在完成这种结合后释放能量。如果条件适当，此能量会以光子的形式释放，该器件就成为光发装置——发光二极管（Light Emitting Diode，LED）。这种器件同样具有坚固耐用、小型紧凑、价格低廉和低压工作的优点。LED已经得到非常广泛的应用。