光学中的波动性及光速的计算方法

1864年，克拉克·麦克斯韦（Clerk Maxwell）就能够表示电磁学定律以证明电场和磁场的对称依存性。为了实现对称性，必须增加一种新的设想：将一个变化的电场（即使是在自由空间中）引入到磁场中。正如法拉第（Faraday）感应定律所述，将一个磁场引入到电场中已经是众所周知的。

现在，每一种场都可以引入到另一种场中。显然，从概念上讲，两种场彼此互相支撑，并作为一种波进行传播是可能的。麦克斯韦（Maxwell）方程将这种思想公式化，并且可以对一种波方程式求导（参考本书附录Ⅰ）。

该波方程可以得到一个与某确定速度的电磁波相对应的自由空间解，其速度取决于自由空间的已知电场性质和磁场性质，因此可由此进行计算。计算得到的结果是一个非常接近已知光速的值，以致可以清楚地将光与这些波区分开，从而确定为一种电磁现象。

通过对麦克斯韦方程的详细研究可以推导出光的所有重要特征，在此限于对几种基本性质的讨论。

如果取笛卡儿（Cartesian）坐标系的轴是Ox、Oy和Oz（见图1.1），就可以得到自由空间方程式正弦形式的简单解：

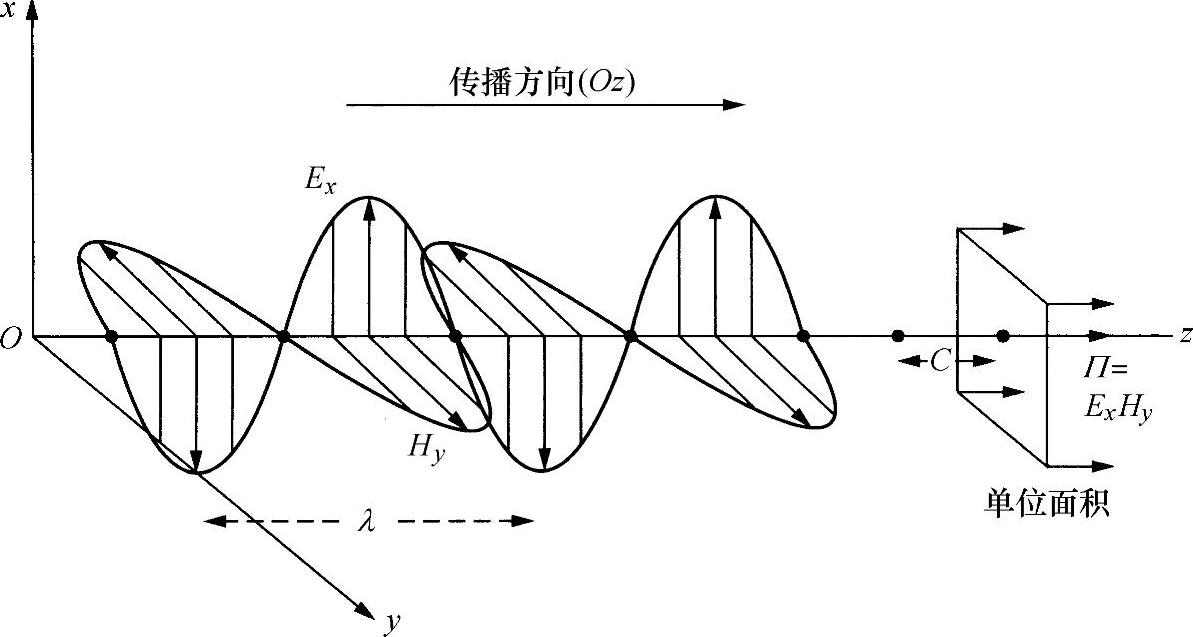
图1.1　正弦形式的电磁波

E_x=E₀exp[i（ωt-kz）]

H_y=H₀exp[i（ωt-kz）] （1.1）

这两个方程式描述了在xz平面内以正弦形式（时间为t，距离为z）振动的电场（E_x）和在yz平面内振动的磁场（H_y），并在Oz方向上传播的一束波。两种场在方向上正交，但具有相同相位，正如麦克斯韦方程的形式所要求的：只有这些条件得以满足，两种场才能彼此相互支撑。还注意到，两种场是在与传播方向Oz垂直的方向上振动的，电磁波是横波。

式（1.1）所描述的波的频率为

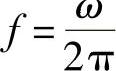
其波长为

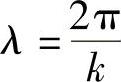
式中，ω和k分别为角频率和波数。由于每秒都有f个波长为λ的光波通过Oz轴上的某一点，很清楚，波的速度为

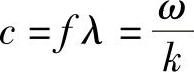
自由空间波方程式表明，该速度应定义如下：

式中，ε₀为自由空间的介电常数；μ₀为自由空间的磁导率（或导磁系数）。电场和磁场都会产生机械力而使两者耦合在一起，但与式（1.2）无关，所以，也就与一个普通的参数力相关，而彼此联系起来。通过这种“力耦合”可以计算出ε₀μ₀的乘积，进而利用式（1.2）依次得到c₀值。因此，利用麦克斯韦（Maxwell）方程就能够确定由电磁波组成的自由空间中的光。

然而，对于电中性（ρ=0）和不会产生电流（j=0）的介质，会保证Maxwell方程自由空间的对称性。一般类型的材料，例如电介质材料，可以满足这些条件。这类材料包括大量的光学介质。在这些介质中，波的速度为

c=（ε_Rε₀μ_Rμ₀）^-1/2 （1.3）

式中，ε_R为介质的相对介电常数（或介电常数）；μ_R为相对磁导率。ε_R和μ_R分别是由介质存在引起的电效应和磁效应增强的量度。的确，对于涉及力场中新的参数时处理起来非常方便，例如下式：(www.xing528.com)

D=ε_Rε₀E

B=μ_Rμ₀H

式中，D为电位移；B为介质的磁感应，分别称为电通量密度和磁通量密度。

根据式（1.3），材料介质中的光速也可以写为

式中，c₀为光在自由空间中的速度，由试验确定的光速值为2.997925×10⁸m/s。对大部分重要的光学介质，μ_R≈1，ε_R>1（因此，称为“介电质”），同时，注意到，这些材料又是电绝缘体，为此可以将式（1.4）写成如下形式：

注意到，由于ε_R>1，所以，c要比c₀小。因此，一种光学材料的折射率n就是光在介质中传播比在自由空间中慢多少的量度，并定义为

由式（1.5）得

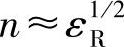
该式将光学介质的光学特性与其原子结构联系在一起，这是一个非常重要的关系。由于该场能使原子中的电子从其平衡位置相对于核子有所移动，所以，该介质的电场效应得到增强，从而产生一个额外的场，使原来的场有效地得以放大。对光波（当然，具有电场分量）传播影响的详细分析将在本书第4章讨论，但马上可以得到两个重要结论：首先，很明显，材料折射率的值取决于传播波的电磁场与介质中原子和分子相互作用的方式；其次，由于已经知道共振频率与原子中电子的结合方式有关，由此可以断定ε与频率相关。n（因此，也包括光波速度）随频率变化是众所周知的现象——光学色散。这在光子学系统中是非常重要的，不仅因为所有的实际光源发射出一宽范围的不同光学频率的光，而且每一个频率都有自己的折射率值。

现在，介绍光波中能量和功率问题。观察许多机械效应，例如真空中导电叶片一侧受到光的照射（见图1.2）会受力旋转，那么显然光波是携带能量的。通过研究波的电磁场对导体的作用，就可以得到这种效应的简单波图。电场会产生真正的电流，并沿电场方向流过导体（对导体中的“自由”电荷作用），因此该电流受到波的正交电磁场的影响。在磁场中，与电流流动方向垂直放置的载流导体会在与该磁场和由弗莱明（Fleming）左手定律确定的方向（幸运的是，该方向就是光波的传播方向）上的电流（电动机原理）两者都垂直的方向上产生一个力。因此，对导体的作用等效于高能粒子在波的传播方向上的撞击作用，换句话说，等效于能量在该方向上的传输。

可以进一步阐述上面的解释：电流正比于电场，力正比于电流和磁场的乘积，因此，能量流（即，与传播方向相垂直的单位面积上能量传输的速率）恰好等于两个的矢量积：

Π=E×H

两个矢量的矢量积可以得到另一个矢量，其振幅是两个矢量振幅的积乘以其方向夹角的正弦。例如sin90°=1，则位于与两个矢量正交的方向上，是从第一个矢量旋转到第二个矢量沿着由右手螺旋定则确定的直线方向。这些矢量常常是以一种非常便于定义这种乘积的方式组合的。

图1.2　光照射一片导电叶片会产生力

显然，如果E和H同相，对于自由空间中传播的电磁波，则矢量积永远是正的。Π是众所周知的坡印廷（Poynting）矢量。在本书附录Ⅰ中，还可以了解到，如果是一束E正比于H的传播波，则垂直于传播方向上通过单位面积的功率与E或H量值的二次方成正比。在本书第2章将完整讨论量值间的关系，但在此一定要注意。这就意味着是单位面积上功率的度量（该量定义为波的强度，有时称为辐照度），是对E或H的直接测量（见图1.1）。由于这种方法能够使人们通过简单实验（即光功率的测量）就对光与原子结构中电子的相互作用过程获得一种控制手段，所以，这是一种很有价值的推论性过程。其原因在于人们认为原子内部是电场和磁场对运动的电荷在起作用。

很明显，光学强度的单位是瓦每平方米（W/m²）。