线性代数第2版：向量的内积和正交

在前面的向量空间中，向量之间的运算只限于线性运算，而几何空间作为其具体模型，还有很多概念和性质没有得到推广，例如在空间解析几何中曾利用向量的数量积讨论过向量的垂直等几何问题.下面在n维向量空间中来讨论类似的问题.

定义5　设n维向量α=（a1，a2，…，an）T，β=（b1，b2，…，bn）T，定义α与β的内积为

特别地，当内积αTβ=0时，称α与β是正交的，否则称为不正交.

例如，当n=3时，3维向量α=（a1，a2，a3）T，β=（b1，b2，b3）T的内积

αTβ=a1b1+a2b2+a3b3

就是几何空间中的数量积，αTβ=0则表示向量α与β垂直.

易证内积具有以下性质（设α，β，γ∈Rn，λ∈R）.

（1）对称性：αTβ=βTα.

（2）齐次性：（λαT）β=λαTβ.

（3）可加性：（α+β）Tγ=αTγ+βTγ.

（4）非负规范性：αTα≥0，当且仅当α=0时，αTα=0.

利用向量内积的非负规范性，可以定义n维向量的长度的定义.

定义6　设n维向量α=（a1，a2，…，an）T，令，则称非负实数为向量α的长度.当时，称α是n维单位向量.

一般地，当非零向量α不是单位向量时，可令，使，此过程称为把非零向量α单位化.

n维向量的长度具有以下性质（设α，β∈Rn，k∈R）.

（1）非负性：，当且仅当α=0时.

（2）齐次性：.

（3）三角不等式：|α+β|≤|α|+|β|.

（4）柯西-施瓦茨不等式，且等号成立的充要条件是α与β线性相关.

由柯西-施瓦茨不等式，有以下定义.(www.xing528.com)

定义7　设n维向量α与β满足，则称为n维向量α与β的夹角.

由定义7知，当n维向量α与β正交时，它们的夹角.

定义8　若向量组α1，α2，…，αs中的向量两两正交，则称该向量组是一个正交向量组；若向量组α1，α2，…，αs中的任一向量与向量组β1，β2，…，βt中的任一向量两两正交，则称两向量组是相互正交的.

例4　试证n维行向量组e1=（1，0，…，0），e2=（0，1，0，…，0），…，en=（0，…，0，1）是一个正交向量组.

证　因为ei中除了第i个分量为1外其余分量都是零，所以

所以向量组e1，e2，…，en两两正交.

例5　设m×n矩阵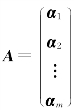，其中n维向量α1，α2，…，αm为矩阵A的行向量组，若r（A）=r，且列向量组β1，β2，…，βn-r为齐次方程组Ax=0的基础解系，则向量组α1，α2，…，αm与β1，β2，…，βn-r是相互正交的.

证　因为β1，β2，…，βn-r为齐次方程组Ax=0的基础解系，所以

Aβj=0　（j=1，2，…，n-r）

于是αiβj=0（i=1，2，…，m；j=1，2，…，n-r），所以向量组α1，α2，…，αm与β1，β2，…，βn-r是相互正交的.

定理1　非零的正交向量组一定线性无关.

证　设α1，α2，…，αs为给定的正交向量组，假设存在一组数k1，k2，…，ks使得下式成立

k1α1+k2α2+…+ksαs=0.

若用与上式作内积，有

因为　αi≠0，

所以　

从而必有　ki=0　（i=1，2，…，s），

即证正交向量组α1，α2，…，αs线性无关.