向量空间的基、维数、坐标

定义2设V是向量空间，若向量组α1，α2，…，αr∈V，且满足下面两个条件.

（1）α1，α2，…，αr线性无关.

（2）V中任一向量都可由α1，α2，…，αr线性表示.

则称向量组α1，α2，…，αr为向量空间V的一组基，数r称为向量空间V的维数，记为dimV=r，并称V为r维向量空间.

注：（1）只含零向量的向量空间称为0维向量空间，它没有基.

（2）若把向量空间V看作向量组，则V的基就是向量组的极大无关组，V的维数就是向量组的秩.

（3）若向量组α1，α2，…，αr是向量空间V的一组基，则V就是由α1，α2，…，αr所生成的向量空间.

例如，在中，基本单位向量组

e1=（1，0，…，0），e2=（0，1，0，…，0），…，en=（0，…，0，1）

就是Rn的一组基，且dimRn=n.一般把e1，e2，…，en称为Rn的自然基.

例1　证明向量组

α1=（1，2，3，4）T，α2=（0，1，-1，2）T，α3=（0，0，2，3）T，α4=（0，0，0，5）T

是R4的一组基.

证　由于

所以α1，α2，α3，α4线性无关，所以α1，α2，α3，α4是R4的一组基.

定义3　设α1，α2，…，αr是向量空间V的一组基，任取β∈V，则β可唯一表示为

由组合系数构成的向量x=（k1，k2，…，kr）T称为β关于基α1，α2，…，αr的坐标向量，简称坐标.

一般坐标向量习惯性用列向量表示，实质上，式（3.5.1）只是一种形式记法，仅仅是从形式上将向量β表示为一个行向量与一个列向量之积，一般来说不具有实际意义.

例2　设.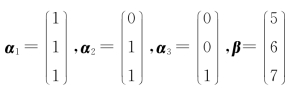

（1）证明：α1，α2，α3是R3的一组基.(www.xing528.com)

（2）求β关于基α1，α2，α3的坐标.

解　（1）由于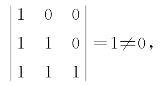　

而　dimR3=3，

所以α1，α2，α3是R3的一组基.

（2）由于　

得β=5α1+α2+α3，

可知β关于基α1，α2，α3的坐标为（5，1，1）T.

定义4　设α1，α2，…，αr和β1，β2，…，βr是向量空间V的两组基，由于α1，α2，…，αr是向量空间V的一组基，所以存在唯一的矩阵Cr×r，使（β1，β2，…，βr）=（α1，α2，…，αr）Cr×r，则把矩阵Cr×r称为从基α1，α2，…，αr到基β1，β2，…，βr的过渡矩阵（基变换矩阵）.

过渡矩阵Cr×r具有如下性质.

（1）矩阵Cr×r的第i列是向量βi关于基α1，α2，…，αr的坐标.

（2）Cr×r是可逆的，且（Cr×r）-1是β1，β2，…，βr到α1，α2，…，αr的过渡矩阵.

例3　取定R3中的一个基α1，α2，α3，再取一个新基β1，β2，β3，设A=（α1，α2，α3），B=（β1，β2，β3），求旧基α1，α2，α3到新基β1，β2，β3的过渡矩阵，并求向量在两个基中的坐标之间的关系式（坐标变换公式）.

解　因为　（α1，α2，α3）=（e1，e2，e3）A，

（e1，e2，e3）=（α1，α2，α3）A-1，

其中e1，e2，e3为R3的自然基.

所以　（β1，β2，β3）=（e1，e2，e3）B

=（α1，α2，α3）A-1B，

即旧基α1，α2，α3到新基β1，β2，β3的过渡矩阵为A-1B.

设R3中任意一个向量为α，α在旧基α1，α2，α3和新基β1，β2，β3中的坐标分别为（x1，x2，x3）T和（y1，y2，y3）T，即