非齐次线性方程组解的结构

设有非齐次线性方程组

它也可写作矩阵方程

矩阵方程（3.4.6）的解也就是方程组（3.4.5）的解向量，它具有如下性质.

性质3　设x=η1及x=η2都是Ax=b的解，则x=η1-η2为对应的齐次线性方程组Ax=0的解.

证A（η1-η2）=Aη1-Aη2=b-b=0，

即x=η1-η2满足方程组Ax=0.

性质4　设x=η是方程组Ax=b的解，x=ξ是方程组Ax=0的解，则x=ξ+η仍是方程组Ax=b的解.

证A（ξ+η）=Aξ+Aη=0+b=b，

即x=ξ+η满足方程组Ax=b.

由性质3可知，若求得Ax=b的一个解η*，则Ax=b的任一解总可表示为x=ξ+η*，其中x=ξ为Ax=0的解，又若Ax=0的通解为

x=C1ξ1+C2ξ2+…+Cn-rξn-r，

则Ax=b的任一解总可表示为

x=C1ξ1+C2ξ2+…+Cn-rξn-r+η*.

而由性质4可知，对任意常数C1，C2，…，Cn-r，上式总是Ax=b的解，于是方程Ax=b的通解为

x=C1ξ1+C2ξ2+…+Cn-rξn-r+η*（C1，C2，…，Cn-r为任意常数），

其中ξ1，ξ2，…，ξn-r是Ax=0的基础解系.(www.xing528.com)

例4　求方程组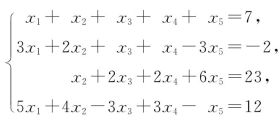的通解.

解　对方程组的增广矩阵实施初等行变换，得

所以方程组有无穷多解，且

取x4=x5=0，则

x1=-16，x2=23，

即得原方程组的一个特解η*=（-16，23，0，0，0）T.

在对应的齐次线性方程组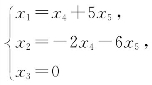中取

得齐次方程组的基础解系为

于是原非齐次方程组的通解为

例5　设四元非齐次线性方程组Ax=b的系数矩阵A的秩为3，已知它的三个解向量为η1，η2，η3，其中

求该方程组的通解.

解　由已知得，方程组Ax=b对应的齐次线性方程组Ax=0的基础解系含4-3=1个向量，所以Ax=0的任何一个非零解都可作为其基础解系.

是Ax=0的非零解，可作为其基础解系.

所以方程组Ax=b的通解为