齐次线性方程组的解结构

则方程组（3.4.1）可写成矩阵方程

若x1=ξ11，x2=ξ12，…，xn=ξ1n为方程组（3.4.1）的解，则

称为方程组（3.4.1）的解向量，它也就是矩阵方程（3.4.2）的解.

根据矩阵方程（3.4.2），来讨论解向量的性质.

性质1　若x=ξ1，x=ξ2为方程（3.4.2）的解，则x=ξ1+ξ2也是方程（3.4.2）的解.

只要验证x=ξ1+ξ2满足方程式A（ξ1+ξ2）=Aξ1+Aξ2=0+0=0即可.

性质2　若x=ξ1为方程（3.4.2）的解，k为实数，则x=kξ1也是方程（3.4.2）的解.

证　A（kξ1）=k（Aξ1）=k0=0.

把方程（3.4.2）的全部解所组成的集合记作S，如果能求得解集S的一个极大无关组S0：ξ1，ξ2，…，ξt，那么方程（3.4.2）的任一解都可由极大无关组S0线性表示.由上述性质1、2可知，极大无关组S0的任何线性组合x=k1ξ1+…+ktξt都是方程（3.4.2）的解，因此上式便是方程（3.4.2）的通解.

齐次线性方程组的解集的极大无关组称为该齐次线性方程组的基础解系，由上面的讨论可知，要求齐次线性方程组的解集的通解，只要求出它的基础解系即可.

上一章用初等变换的方法求线性方程组的通解，下面用同一方法求齐次线性方程组的基础解系.

设方程组（3.4.1）的系数矩阵A的秩为r，并不妨设A的前r个列向量线性无关，A的行最简形矩阵为

与B对应，即有方程组

把xr+1，…，xn作为自由未知量，并令它们依次等于C1，…，Cn-r（C1，…，Cn-r为任意常数），可得方程组（3.4.1）的通解

把上式记作x=C1ξ1+C2ξ2+…+Cn-rξn-r（C1，…，Cn-r为任意常数）.

可知解集S中的任一向量x能由ξ1，ξ2，…，ξn-r线性表示，又因为矩阵（ξ1，ξ2，…，ξn-r）中有n-r阶子式，所以r（ξ1，ξ2，…，ξn-r）=n-r，所以ξ1，ξ2，…，ξn-r线性无关，根据极大无关组的等价定义，即知ξ1，ξ2，…，ξn-r是解集S的极大无关组，即ξ1，ξ2，…，ξn-r是方程组（3.4.1）的基础解系.

在上面的讨论中，先求出齐次线性方程组的通解，将通解写成向量形式，再从通解求得基础解系，其实也可先求基础解系，再写出通解，这只要在得到方程组（3.4.3）以后，令自由未知量xr+1，xr+2，…，xn分别取下列n-r组数

由方程组（3.4.3）依次可得

合起来便得基础解系

依据以上的讨论，还可推得定理1.

定理1　设m×n矩阵A的秩r（A）=r，则n元齐次线性方程组Ax=0的解集S的秩rS=n-r.

当r（A）=n时，方程组（3.4.1）只有零解，没有基础解系（此时解集S只含一个零向量）；当r（A）=r＜n时，由定理1可知方程组（3.4.1）的基础解系含n-r个向量，因此，由极大无关组的性质可知，方程组（3.4.1）的任何n-r个线性无关的解都可构成它的基础解系.由此可知齐次线性方程组的基础解系并不是唯一的，它的通解的形式也不是唯一的.

例1　求齐次线性方程组

的基础解系与通解.

解　将方程组的系数矩阵A化为行最简形矩阵

从而知r（A）=3，所以基础解系中有n-r（A）=5-3=2个解向量，由行最简形矩阵知

令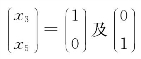，得原方程组的基础解系为

于是通解为

本章3.1节中线性方程组的解法是从方程组（3.4.4）写出通解，将通解写成向量形式，再从通解的表达式即可得基础解系.现在从方程组（3.4.4）先取基础解系，再写出通解，两种解法其实没有多少区别.

根据方程组（3.4.4），如果取(www.xing528.com)

即得不同的基础解系η1，η2.

从而得通解

x=C1η1+C2η2.

显然ξ1，ξ2与η1，η2是等价的，两个通解虽然形式不一样，但都含两个任意常数，且都可表示方程组的任一解.

例2　设Am×nBn×t=O，证明：r（A）+r（B）≤n.

证　记　B=（b1，b2，…，bt），

则A（b1，b2，…，bt）=（0，0，…，0），

即Abi=0（i=1，2，…，t）.

表明矩阵B的t个列向量都是齐次线性方程组Ax=0的解，记方程组Ax=0的解集为S，由

bi∈S，

知r（b1，b2，…，bt）≤rS，

即r（B）≤rS.

而由定理1有

r（A）+rS=n，

所以　r（A）+r（B）≤n.

例3　证明：r（ATA）=r（A）（A为实矩阵）.

证　设A为m×n矩阵，x为n维列向量.

若x满足Ax=0，则

AT（Ax）=0，即（ATA）x=0；

若x满足（ATA）x=0，则

xT（ATA）x=0，即（Ax）T（Ax）=0.

令Ax=（b1，b2，…，bm）T，

于是　

所以必有　b1=b2=…=bm=0，

即必有　Ax=0.

综上可知方程组Ax=0与（ATA）x=0同解，因此

r（ATA）=r（A）.

注：定理1揭示了矩阵A的秩与Ax=0的解之间的关系，它不仅对求Ax=0的解有重要的意义，而且如例2、例3所表明的那样，可以通过研究线性方程组的解来讨论矩阵的秩.