第1章介绍了利用行列式的性质求解n个未知量n个方程的非齐次线性方程组的克莱姆法则.但是当方程的个数与未知量的个数不同时,没有系数行列式,因此不能利用克莱姆法则来求解这种n个未知量m个方程的非齐次线性方程组.因此回过头来分析一下初等代数中是如何利用消元法求解三元一次方程组的,以便将它推广到n元非齐次线性方程组的求解中去.首先看一个利用高斯消元法(简称消元法)求解的简单例子.
例1 用消元法求解下列线性方程组

解 将原方程组中的方程①与②交换,得

再分别用(-2)与(-1)乘以方程组(3.1.2)中的方程①后加到方程②与③,可得

再将方程组(3.1.3)中的方程③乘以(-1),得

通常把方程组(3.1.1)变为方程组(3.1.4)的过程称为消元过程,此时对应于方程组(3.1.4)的系数矩阵是一个行阶梯形矩阵,因此称方程组(3.1.4)为行阶梯形方程组.
从上述解题过程可知,用消元法求解线性方程组的具体做法就是对方程组反复实施下面的三种变换.
(1)交换某两个方程的次序.
(2)用一个非零常数乘某一个方程的两边.(https://www.xing528.com)
(3)将一个方程的倍数加到另一个方程上去.
以上这三种变换称为线性方程组的初等变换.消元法的目的就是利用方程组的初等变换将原方程组化为阶梯形方程组(3.1.4).由于方程组(3.1.4)也可用类似的初等变换还原为原方程组,因此,这个阶梯形方程组与原线性方程组同解.进一步地,对这个同解方程组继续施以初等变换,可得
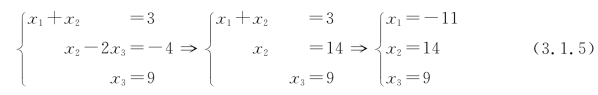
通常把上面的这一求解过程称为回代过程.而消元过程和回代过程合起来就称为高斯消元法(简称消元法).
从第2章可知,线性方程组与其增广矩阵是一一对应的,则上述对方程组的初等变换实际上等价于增广矩阵的初等行变换,详见表3-1.
表3-1 方程组的初等变换与增广矩阵的初等行变换
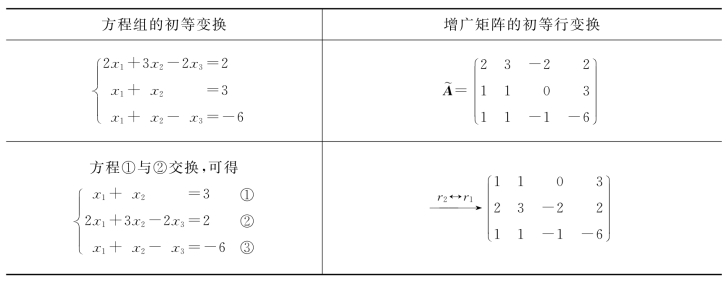
续表

注:高斯消元法的思想早在我国古代数学专著《九章算术》上面就有完整的记载,这要比西方早一千多年,是值得骄傲的伟大成就.
由表3-1可以发现,用高斯消元法求解线性方程组(3.1.1)的过程,实际上就是把线性方程组的增广矩阵施以初等行变换的过程,实施初等行变换的目的是为了把增广矩阵化为行阶梯形矩阵,最终再化为行最简形矩阵,而行最简形矩阵代表的方程组的解即为方程组(3.1.5)的解.
注:将方程组(3.1.1)的增广矩阵化为相应的行阶梯形矩阵并不是唯一的,所以将方程组(3.1.1)化为相应的行阶梯形方程组也不是唯一的,但行最简形矩阵是唯一的.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




