定义1 在m×n矩阵A=（aij）m×n中，任取k行k列（1≤k≤m，1≤k≤n），位于这些行列交叉处的k2个元素，不改变它们在A中所处的位置次序而得到的k阶行列式，称为矩阵A的k阶子式.
注：m×n矩阵A的k阶子式共有
个.
取1、2行和1、3列相交处的元素组成A的一个2阶子式
设A为m×n矩阵，由定义1知，当A=O时，它的任何子式都为零；当A≠O时，它至少有一个元素不为零，即它至少有一个1阶子式不为零.这时再考察2阶子式，若A中有2阶子式不为零，则往下考察3阶子式，如此进行下去，最后必达到A中有r阶子式不为零，而再没有比r更高阶的不为零的子式.这个不为零的子式的最高阶数r反映了矩阵A内在的重要特征，在矩阵的理论与应用中都有重要意义.
A中有2阶子式
，但它的任何3阶子式都为零，即A不为零的子式的最高阶数r=2.
定义2 设矩阵A为m×n矩阵，如果A中不为零的子式的最高阶数为r，即存在r阶子式不为零，而任何r+1阶子式都为零，则称r为矩阵A的秩，记作r（A）=r.零矩阵的秩规定为0.
上例中，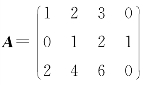
，则有r（A）=2.
由矩阵秩的定义与行列式的性质易知，矩阵的秩具有如下性质.
（1）在A中当所有r+1阶子式全等于0时，所有高于r+1阶子式也全等于0，因此把r阶非零子式称为A的最高阶非零子式，而A的秩r（A）就是A的非零子式的最高阶数.
（2）若矩阵A中有某个s阶子式不等于0，则r（A）≥s；若矩阵A中所有t阶子式全等于0，则r（A）＜t.
（3）
.
（4）r（A）=r（AT），r（λA）=r（A）（λ≠0）.(www.xing528.com)
（5）对于n阶矩阵A，由于n阶子式只有一个|A|，若|A|≠0时，r（A）=n；若|A|=0时，r（A）＜n.所以可逆矩阵（非奇异矩阵）又叫满秩矩阵，不可逆矩阵（奇异矩阵）又叫降秩矩阵.
例1 求下列矩阵的秩：
解 （1）因为 |A|=6≠0，
所以A的不为零的子式的最高阶数是3，所以
r（A）=3.
（2）先考察矩阵B的四个3阶子式
然而存在2阶子式
所以 r（B）=2.
（3）因为C为3×5矩阵，所以其子式最高只能为3阶，而1、2、4列所构成的3阶子式
所以 r（C）=3.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
