定义6 对单位矩阵I施以一次初等变换得到的矩阵称为初等矩阵.
因此,三种初等变换分别对应着三种初等矩阵.
(1)I的第i,j行(列)互换得到的矩阵,记为
(2)I的第i行(列)乘以非零数k得到的矩阵记为
(3)I的第j行乘以数k加到第i行上或I的第i列乘以数k加到第j列上得到的矩阵记为
不难验证,初等矩阵具有下列性质.
(1)初等矩阵都是可逆矩阵,它们的逆矩阵还是同类型的初等矩阵,并且
(I(i,j))-1=I(i,j),
(I((k)i))-1=I((k-1)i),
(I(i+(k)j))-1=I(i+(-k)j).
(2)|I(i,j)|=-1,
|I((k)i)|=k,
|I(i+(k)j)|=1.
定理2 对矩阵A施行一次初等行变换,相当于用同种类型的初等矩阵左乘A;对矩阵A施行一次初等列变换,相当于用同种类型的初等矩阵右乘A.
例如,设A=(aij)3×3,把A的第1行乘以k加到第3行上去,相当于(https://www.xing528.com)
由定理2知,存在初等矩阵P1,P2,…,Ps和Q1,Q2,…,Qt,使得
若A为n阶可逆方阵,则|A|≠0,从而A化为标准形矩阵后不可能有零行和零列,所以r=n.即
Ps…P1AQ1…Qt=In,
于是
由初等矩阵的性质知,等式右边均为初等矩阵.
定理3 可逆矩阵A可以表示为有限个初等矩阵的乘积,并且可逆矩阵A可以只用初等行(列)变换化为单位矩阵.
若A可逆,则A-1可逆且可以表示为有限个初等矩阵的乘积,即
式(2.5.1)表明对A实施若干次初等行变换化为单位矩阵I,式(2.5.2)表明对I实施同样的初等行变换可以化为A-1,P1P2…Ps(A,I)=(I,A-1).
所以可以得到一种求逆矩阵的方法.
对于n阶可逆矩阵A,作一个n×2n的分块矩阵(A,I),对其实施初等行变换,将分块矩阵(A,I)的子块A化为I,与此同时子块I化为A-1,即
这就是求逆矩阵的初等变换法.
类似地,也可以用初等列变换求逆矩阵,即
例2 用初等变换法求矩阵A的逆矩阵,其中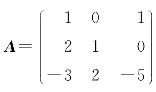 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




