【摘要】：，n），那么就称这个矩阵为对称矩阵，例如，只有一行的矩阵A=（a1，a2，…，an）称为行矩阵或行向量.只有一列的矩阵称为列矩阵或列向量.例3对于n元线性方程组有如下几个有用的矩阵：其中，A称为线性方程组的系数矩阵，x称为未知量矩阵，b称为常数项矩阵，称为线性方程组的增广矩阵.
所有元素都是零的矩阵称为零矩阵，记做O，即
注意不同型的零矩阵是不同的.
若矩阵A=（aij）的行数与列数都等于n，则称矩阵A为n阶矩阵或n阶方阵，n阶矩阵A也记作An.
1阶矩阵（a）就是数a，即（a）=a.
注：n阶矩阵仅仅是由n2个元素排成的一个正方形表，与n阶行列式不同.
若n阶矩阵A=（aij）主对角线上的元素全为1，其余元素都为零，则称这个矩阵为n阶单位矩阵，记作In（或En），即
注：零矩阵和单位矩阵这两类特殊矩阵在后续一些结论的证明和定义中起着重要的作用.
若n阶方阵不在主对角线上的元素皆为零，则称这个矩阵为对角矩阵，记为
主对角线上是相同的非零元素，其余元素全为零的方阵称为数量矩阵，即(www.xing528.com)
主对角线下方元素皆为零的方阵称为上三角矩阵，即
主对角线上方元素皆为零的方阵称为下三角矩阵.即
对于n阶矩阵A=（aij），如果aij=aji（i，j=1，2，…，n），那么就称这个矩阵为对称矩阵，例如，
只有一行的矩阵A=（a1，a2，…，an）称为行矩阵或行向量.
只有一列的矩阵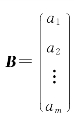
称为列矩阵或列向量.
例3 对于n元线性方程组
有如下几个有用的矩阵：
其中，A称为线性方程组的系数矩阵，x称为未知量矩阵，b称为常数项矩阵，
称为线性方程组的增广矩阵.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
