线性代数（第2版）：克莱姆法则的应用

应用行列式解决线性方程组的求解问题，在这节中只考虑方程个数与未知量的个数相等的情形，这是一个重要的情形，至于更一般的情形留到第3章讨论.

在引入克莱姆法则之前，先介绍有关n元线性方程组的概念.

含有n个未知量、n个方程的线性方程组

称为n元线性方程组.当其右端的常数项bi（i=1，2，…，n）不全为零时，线性方程组（1.4.1）称为非齐次线性方程组；当bi（i=1，2，…，n）全为零时，线性方程组（1.4.1）称为齐次线性方程组，即

线性方程组（1.4.1）的系数aij（i，j=1，2，…，n）按原顺序构成的行列式称为该方程组的系数行列式，即

定理1　（克莱姆法则）若线性方程组（1.4.1）的系数行列式D≠0，则线性方程组（1.4.1）有唯一解，其解为

其中，Dj（j=1，2，…，n）是把D中第j列元素a1j，a2j，…，anj换成方程组（1.4.1）的常数项b1，b2，…，bn，而其余各列保持不变所得到的行列式.

证　以行列式D的第j（j=1，2，…，n）列元素的代数余子式A1j，A2j，…，Anj分别乘以方程组（1.4.1）的第1，第2，…，第n个方程，然后相加，得

（a11A1j+a21A2j+…+an1Anj）x1+…+（a1jA1j+a2jA2j+…+anjAnj）xj+…+（a1nA1j+a2nA2j+…+annAnj）xn=b1A1j+b2A2j+…+bnAnj

由1.3节的结论，xj的系数等于D，xs（s≠j）的系数等于零.等号右端等于D中第j列元素换成常数列b1，b2，…，bn后得到的行列式Dj，即

如果方程组（1.4.1）有解，则其解必满足式（1.4.4），而当D≠0时，式（1.4.4）只有形如式（1.4.3）的解.

另一方面，将式（1.4.3）代入方程组（1.4.1），容易验证它满足方程组（1.4.1），所以式（1.4.3）是方程组（1.4.1）的解.(www.xing528.com)

综上所述，当方程组（1.4.1）的系数行列式D≠0时，有且仅有唯一解

注：（1）用克莱姆法则求线性方程组的解时，计算量是比较大的.对具体的数字线性方程组，当未知数较多时可用计算机来求解，后面介绍了利用MATLAB软件来求解线性方程组的方法.

（2）克莱姆法则在一定条件下给出了线性方程组解的存在性、唯一性，但其在实际计算方面的应用较少，然而在理论上具有重大的价值.

对齐次线性方程组（1.4.2），易见x1=x2=…=xn=0一定是该方程组的解，称其为齐次线性方程组（1.4.2）的零解.把定理1应用于齐次线性方程组（1.4.2），可得到下列结论.

定理2　如果齐次线性方程组（1.4.2）的系数行列式D≠0，则齐次线性方程组（1.4.2）只有零解.

推论　如果齐次方程组（1.4.2）有非零解，则它的系数行列式D=0.

注：第3章还将进一步证明，如果齐次线性方程组（1.4.2）的系数行列式D=0，则齐次线性方程组（1.4.2）必有非零解.

例1　用克莱姆法则求方程组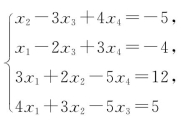的解.

例2　已知齐次线性方程组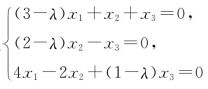有非零解，求λ的值.

解　因为齐次线性方程组有非零解，所以其系数行列式为零，

所以　λ=3或λ=4或λ=-1.