【摘要】：定义2在n阶行列式D中，任意选定k行（i1＜i2＜…＜ik）k列（j1＜j2＜…=n-1D2=n.注：本节例题计算行列式之前要先观察其元素的特点，再根据其特点来采取不同的计算方法.
定义2 在n阶行列式D中，任意选定k行（i1＜i2＜…＜ik）k列（j1＜j2＜…＜jk）（1≤k≤n），位于这些行和列交叉处的k2个元素，按原来顺序构成一个k阶行列式M，称为D的一个k阶子式.划去这k行k列，余下的元素按原来的顺序构成n-k阶行列式称为M的余子式，记为N，称
为M的代数余子式.
注：行列式D的k阶子式与其代数余子式之间有类似行列式按行（列）展开的性质.
定理2（拉普拉斯定理）在n阶行列式D中，任意取定k行（列）（1≤k≤n-1），由这k行（列）元素组成的所有k阶子式与它们的代数余子式的乘积之和等于行列式D.
例6 用拉普拉斯定理计算行列式
.
解 按第一行和第二行展开，则有3个非零的2阶子式，
例7 计算5阶行列式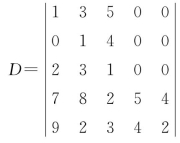
.
解 选取第一行、第二行和第三行用拉普拉斯定理计算得(www.xing528.com)
注：当行列式中某k行（列）中零元较多时，可用拉普拉斯定理简化计算.
例8 计算2n阶行列式
（其中未写出的元素为0）.
解 用拉普拉斯定理把D2n中的第1行和第2n行展开得
D2n=（a2-b2）D2（n-1），
以此作递推公式得
D2n=（a2-b2）D2（n-1）=…=（a2-b2）n-1D2=（a2-b2）n.
注：本节例题计算行列式之前要先观察其元素的特点，再根据其特点来采取不同的计算方法.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
