线性代数第2版：行列式按某行（列）展开

由于低阶行列式的计算常常比高阶行列式简便，那么思考一个问题：高阶行列式能否转化为低阶行列式进行计算？为解答这个问题，先来看看2阶、3阶行列式之间的关系.

括号中的部分显然可视为三个2阶行列式，将其中的元素按行标、列标从小到大排列位置，则3阶行列式就变为

其中的三个2阶行列式，显然是原来的3阶行列式中分别划出元素a11，a12，a13（即这三个2阶行列式前的乘法因子）所在的行和列后，剩余的元素按照原来的顺序构成的子行列式（简称余子式），分别记为

这样就得到了3阶行列式（1.1.3）按第1行元素的余子式展开，即

D=a11M11-a12M12+a13M13，

式中的“+”“-”号如何确定显然是个问题.发现各项前的“+”“-”号与元素a11、a12、a13的下标之和的奇偶性有关系，即“+”号对应的下标之和为偶数，“-”号对应的下标之和为奇数，所以可引入下面的代数余子式，即

A11=（-1）1+1M11，

A12=（-1）1+2M12，

A13=（-1）1+3M13.

得到了3阶行列式（1.1.3）更加简洁的代数余子式展开

也可按各项中所包含的第一列元素来配对，得到3阶行列式按第一列元素的余子式展开和代数余子式展开

D=a11M11-a21M21+a31M31

同理，3阶行列式也可以按第二、三行（列）元素的余子式和代数余子式展开.

类似地，可定义n阶行列式的余子式和代数余子式，并且推广出n阶行列式的展开定理.

定义1　在n阶行列式D中，将（i，j）元aij所在的第i行和第j列的元素划去后，余下的元素按照原来的相对顺序组成一个n-1阶行列式，称为D中元素aij的余子式，记为Mij，称Aij=（-1）i+jMij为aij的代数余子式.

定理1　设有n阶行列式

定理1表明，行列式D等于它的任一行的各元素与其对应的代数余子式的乘积之和，称式（1.3.1）为行列式的按行展开定理.当然行列式D也可以按列展开，即行列式D等于它的任一列的各元素与其对应的代数余子式的乘积之和，即

推论　行列式中任一行（列）的元素与另一行（列）元素的代数余子式的乘积之和等于零，即

事实上，考虑行列式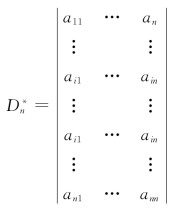，即第j行跟第i行一样，再按第j行展开，

即证.

综上所述，可得到行列式有关代数余子式的展开定理如下：

例1　计算行列式.(www.xing528.com)

分析：第4行有2个零元，所以按第4行展开.

解　D=2×A41+0×A42+0×A43+4×A44=-2M41+4M44=-2×0+4×5=20.

注：实际计算时，如果行列式的某一行或某一列元素中零元素越多，则展开式中真正需要计算的代数余子式就越少，行列式的计算也就越简单，因此常常在利用行列式的展开定理之前先利用行列式的性质，特别是倍加变换，将行列式要展开的那一行（列）化为只有一个元素非零，其余元素都是零（注意此时这一行（列）中的非零元素在哪里无所谓），再按这一行（列）展开，计算量将会减少很多.

例2　计算行列式.

注：在计算高阶行列式时，无须将行列式化为上三角行列式，也可以利用行列式的按行（列）展开定理，就可将高阶行列式降一阶，以此类推，就可把任意高阶行列式最终化为2阶行列式来计算了，这种方法称为降阶法.

例3　计算n+1阶行列式.

解　把第1列至第n列都加到第n+1列上去得

例4　计算n阶行列式.

解　按第1列展开，然后将右端第二项的行列式按第1行展开得

所以　Dn-Dn-1=Dn-1-Dn-2，

由此递推得

Dn-Dn-1=Dn-1-Dn-2=…=D2-D1=3-2=1，

从而　Dn=Dn-1+1=Dn-2+2=…=D1+（n-1）=n+1.

例5　证明行列式

对任意的n（n≥2），Dn等于a1，a2，…，an，这n个数的所有可能的差ai-aj（1≤j＜i≤n）的乘积，即.

式（1.3.2）称为n阶的范德蒙行列式，表示全体同类因子的乘积.

证　对n作归纳法，当n=2时，.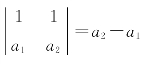

假设对n-1阶范德蒙行列式结论是成立的，现在来看n阶的情形，式（1.3.2）由下而上依次地从每一行减去它上一行的a1倍，有

后面这个行列式是一个n-1阶范德蒙行列式，根据归纳法假设它等于所有可能差aiaj（2≤j＜i≤n）的乘积，而包含a1的差都在前面出现了，因此，结论对n阶范德蒙行列式也成立，根据归纳法，完成了证明.

因此，范德蒙行列式为零的充分必要条件是a1，a2，…，an这n个数中至少有两个数相等.