行列式性质及计算简化方法

直接利用行列式的定义来计算行列式，只有在行列式的阶数较低，或者其元素特殊（如零元较多）时可行，而高阶行列式的计算一般较烦琐.为此，要给出行列式的一些基本性质，以便简化行列式的计算.

定义　将行列式D的行和列交换后得到的新的行列式称为D的转置行列式，记为DT或D＇，即若

性质1　行列式经过转置，其值不变，即对任意n阶行列式有DT=D.

证　设行列式D与其转置行列式DT的（i，j）元分别为aij和bij，则由转置行列式的定义有bij=aji（i，j=1，2，…，n），于是由行列式的定义及其等价定义可得

性质1　说明行列式中行与列具有对等的地位，因此凡是对“行”成立的性质，对“列”也同样成立，反之亦然.

性质2　互换行列式的任意两行（列），行列式变号.

证明略.

一般地，互换行列式的第i行和第j行的这种变换，记作ri↔rj；互换行列式的第i列和第j列的这种变换，记作ci↔cj.

推论1　如果行列式中有两行（列）元素相同，那么行列式的值为零.

性质3　用数k乘行列式D的某一行（列），等于以数k乘以行列式D，即

证明略.

这就是说，行列式中某一行（列）的公因子可以提到行列式的外面，或者说以一数乘以行列式就相当于用这个数乘此行列式的某一行（列）.

一般地，用数k乘行列式的第i行的这种变换，记作kri；用数k乘行列式的第i列的这种变换，记作kci.

特别地，令k=0，则行列式的值为0.说明如果行列式中的某一行（列）全为零，那么行列式的值为零.

推论2　行列式中若有两行（列）元素对应成比例，则此行列式的值为零.

例1　计算行列式.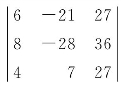

性质4　如果行列式D中某一行（列）的每一个元素都是两个数之和，则D可写为两个行列式之和，即

证明略.

这就是说，如果某一行（列）是两组数的和，那么这个行列式就等于两个行列式的和，而这两个行列式除这一行（列）以外全与原来行列式对应的行（列）一样.(www.xing528.com)

性质5　如果将行列式某一行（列）的所有元素都乘以数k后加到另一行（列）对应位置的元素上，那么行列式的值不变，即

证明略.

一般地，以数k乘第j行加到第i行上的这种变换，称为倍加行变换，记作ri+krj；以数k乘第j列加到第i列上的这种变换，称为倍加列变换，记作ci+kcj.

行列式的计算是一个重要的问题，也是一个复杂的问题.这一节提供计算行列式的一种常用方法，即利用上述的各种性质，特别是倍加变换法，将一般行列式变换为值易求的特殊行列式，如上（下）三角行列式.由数学归纳法可以证明，任意行列式经过有限次倍加变换法，都可以转换为一个上（下）三角行列式，而上（下）三角行列式的值等于其主对角线上元素的乘积.

例2　计算行列式.

例3　计算行列式.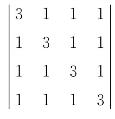

解　注意到行列式各列的4个数的和都是6，所以把第2、3、4行同时加到第1行，可提出公因子6，再由各行减去第1行即可化为上三角行列式，即

注：在计算过程中，将其他行（列）统统加到某一行（列）上去，这个小技巧在计算这类行列式时经常会用到.

与例3中这种行列式对应的n阶行列式为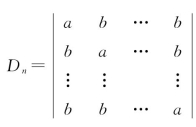，通常称之为ab型行列式，可依例3的方法得到一般结果：

例4　（X型行列式）计算6阶行列式.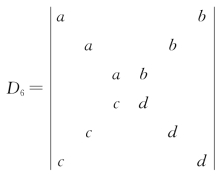

分析：如果能消去X型行列式的半条对角线，显然就变成了三角行列式.

解　当a≠0时，依此将第1、2、3行的倍分别加到第6、5、4行，并记

当a=0时，行列式退化为次下三角行列式，又ad=0，即

D6=（-1）τ（654321）b3c3

=（-1）15b3c3

=-b3c3

=（ad-bc）3.

综上所述，可知　D6=（ad-bc）3.