线性代数第2版：n阶行列式的定义及性质

从2阶、3阶行列式的定义可知，它们都是若干项的代数和，而每一项都是由行列式中位于不同行和不同列的元素的乘积所构成的，并且展开式恰恰就是由所有的这些乘积组成的，因此推测n阶行列式应该具有如下特点.

（1）n阶行列式由n！项的代数和构成.

（2）n阶行列式的每项都是该行列式中的不同行不同列的n个元素的乘积.

（3）n阶行列式的每一项都有符号规律，有的取正，有的取负，正负各占一半.

为了进一步说清这些符号的内在规律，给出以下的有关概念.

定义3　由1，2，3，…，n组成的一个有序数列称为n级排列.

例如，12345是一个5级排列，34512是一个5级排列，2341是一个4级排列.

显然，n级排列的总数是n（n-1）（n-2）…2·1=n！，123…n也是一个n级排列，这个排列具有自然顺序，就是按递增的顺序排起来的，称为自然排列，而其他排列都或多或少地破坏了自然顺序.

定义4　在一个排列中，如果一对数的前后位置与大小顺序相反，即较大的数排在了较小的数之前，则称这两个数构成一个逆序.一个n级排列i1i2…in中的逆序的总数就称为这个n级排列的逆序数，记为τ（i1i2…in）.其中逆序数为偶数的排列称为偶排列，逆序数为奇数的排列称为奇排列.

例如，2341中，21，31，41是逆序，2341的逆序数就是3，即τ（2341）=3，这是一个奇排列；而5级排列35421的逆序数是8，即τ（35421）=8，这是一个偶排列.

在3阶行列式（1.1.3）中，有3！项的代数和，有3项取正，3项取负，其中取正号的3项中各元素的列标组成的排列分别为123、231、312，它们的逆序数分别为0、2、2，都是偶数；而取负号的3项中各元素的列标组成的排列分别为321、213、132，逆序数分别为3、1、1，都是奇数.在3阶行列式的展开式中，项的一般形式可写成，其中j1j2j3是123的一个排列，当j1j2j3是偶排列时，对应的项带有正号，当j1j2j3是奇排列时，对应的项带有负号.所以3阶行列式（1.1.3）可写成如下形式：

其中，表示对所有3级排列求和.

定义5　n阶行列式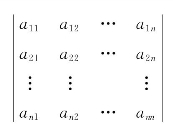等于所有取自不同行不同列的n个元素的乘积的代数和，这里j1j2…jn是1，2，3，…，n的一个n级排列，每一项都按下列规则带有符号：当j1j2…jn是偶排列时，带有正号；当j1j2…jn是奇排列时，带有负号.即

其中，表示对所有n级排列求和，aij（i，j=1，2，…，n）是n阶行列式的（i，j）元，即第i行第j列的元素，称为n阶行列式的一般项.

注：（1）1阶行列式|a|=a，不要与绝对值记号混淆.

（2）n阶行列式的等价定义为

其中，表示对所有n级排列求和.

例2　用行列式定义计算行列式.

解　这个4阶行列式，其主对角线以上的元素全为零，称为4阶下三角行列式，其展开项共有24项，因为行列式的一般项为，若某一项的四个元素乘积中只要有一个元素为零，则该项为零.因此先考虑零元最多的第一行，其中只有a11≠0，所以只能取j1=1，同理，j2=2，j3=3，j4=4，即不为零的项只有a11a22a33a44这一项，且该项的符号为（-1）τ（1234），其中1234为偶排列.所以(www.xing528.com)

一般地，n阶下三角行列式（主对角线以上的元素全为零）

即下三角行列式等于它的主对角线元素的乘积（行列式中从左上角到右下角的主对角线上元素称为主对角元）.

同理，n阶上三角行列式（主对角线以下的元素全为零）

即上三角行列式也等于它的主对角线元素的乘积.

特别地，n阶对角行列式（除主对角元以外的元素全为零）也等于主对角线元素的乘积，即

例3　按定义计算行列式.

解　由于所给行列式的展开项中只含一个非零项

a12a23…an-1，nan1，

而它前面所带符号为

（-1）τ（23…n1）=（-1）n-1，

所以　Dn=（-1）n-1n！.

例4　已知函数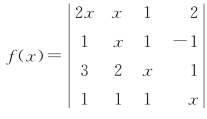，求x4与x3的系数.

解　根据定义，只有对角线上的元素相乘才出现x4，而且这一项带正号，即2x4，所以f（x）的x4系数为2.

同理，含x3的项也只有一项，即

x·1·x·x=x3，

其列标所构成的排列为2134，即

τ（2134）=1，

所以f（x）的含x3的项为-x3，它的系数为-1.