宽频带宽角度电磁散射快速成像

将压缩感知技术应用在雷达成像算法上，主要目的就是降低对回波数据的采样率。在这里，成像算法的主要思路是：首先对每个方位上的信号进行低速数字采样，然后利用压缩感知技术获取每个方位上的距离像，最后利用传统的成像方法得到目标的二维图像。其中，最关键的部分就是低速数字采样和距离像的重构。

一般的雷达成像模型可表示为图6-16所示的形式，图中，f为观测区域，可描述为若干个强散射中心；h为发射信号，通常采用宽频带信号；x为回波信号。常用的未知观测区域成像方法是对发射信号h和回波信号x进行采样，并且采样率严格遵循采样定理，然后利用Fourier变换将信号变换到频域进行处理。但是，采样定理指出：无失真地从离散信号中恢复原信号，其采样速率至少要大于信号带宽。随着信息需求量增加，信号带宽变宽，对采样速率和处理速度要求就越高，给信号的采样、存储、传输和处理等带来了巨大的压力。

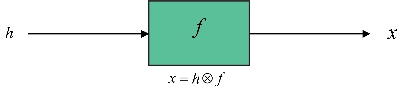
图6-16 雷达成像形式

然而，CS理论认为，遵循Nyquist准则(奈奎斯特准则)对回波信号进行采样，获得的离散序列具有可压缩特性，利用CS技术可使实际采样率远低于Nyquist准则，减轻信号处理的压力，然后解码重构未知区域f。

当所要成像的未知观测区域具有稀疏特性时，可采用基于压缩感知的稀疏成像算法对目标进行成像处理，此时的目标成像处理过程就是目标的后向散射系数重建过程。这里不失一般性，我们先假设雷达接收的回波信号x为一维，则它可由一个稀疏基Ψ将其稀疏化，可表示为

其中，θ即为稀疏目标的后向散射系数。

另外，对于测量矩阵Φ的设计，文献指出，当测量矩阵的每一行有且只有一个非零元素1，并且该值是随机分布在测量矩阵的每一列时，就能以非常高的概率对图像进行完美的重构，例如(www.xing528.com)

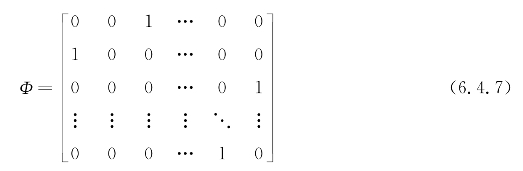
从本质上说，上面测量矩阵的构造其实就是对与其作右乘的矩阵进行随机选行，也就是对稀疏基Ψ进行选行，一般情况下，为了避免两个矩阵相乘运算，我们可以直接地给出抽选过后的稀疏基矩阵。这里还需要指出的是，对于一般的雷达采样机制，常用的降采样的方法都是通过降低距离向采样率或脉冲重复频率的方式来实现，因此，为了方便实现，这个测量矩阵的随机选行可以用等间隔选行来代替。

通常采用压缩感知理论对目标区域进行雷达成像的方法是直接对接收到的回波数据进行解码重构，获得目标的一维距离像，此时的稀疏基函数可根据雷达接收到的回波信号形式来设计，一般雷达接收到的回波信号为

因此，我们可以根据式(6.4.8)中的指数项构造稀疏基Ψ为

只要雷达图像能够被稀疏表示，就可以应用压缩感知理论对其进行解码重构。采用正交匹配追踪等重构算法，获得了每个方位上的一维距离像之后，就可以利用传统的成像方法重构目标的图像。因此，压缩感知雷达技术可在降低采样率的同时实现三维目标成像。