压缩感知重构算法，快速成像与分析

压缩传感理论主要包括信号的稀疏表示、编码测量和重构算法等三个方面。信号的稀疏表示就是将信号投影到正交变换基时，绝大部分变换系数的绝对值很小，所得到的变换向量是稀疏或者近似稀疏的，可以将其看作原始信号的一种简洁表达，这是压缩传感的先验条件，即信号必须在某种变换下可以稀疏表示。通常变换基可以根据信号本身的特点灵活选取，常用的有离散余弦变换基、快速傅立叶变换基、离散小波变换基、Curvelets基、Gabor基以及冗余字典等。在编码测量中，首先，选择稳定的投影矩阵，为了确保信号的线性投影能够保持信号的原始结构，投影矩阵必须满足约束等距性(Restricted Isometry Property，RIP)条件；然后，通过原始信号与测量矩阵的乘积获得原始信号的线性投影测量；最后，运用重构算法由测量值及投影矩阵重构原始信号。信号重构过程一般转换为求解一个最小l0范数的优化问题，解方法主要有最小l1范数法、匹配追踪系列算法、最小全变分方法、迭代阈值算法等。

⇨信号的稀疏表示

CS理论的前提条件是信号具有稀疏性或可压缩性。如果一个信号中只有少数元素是非零的，则该信号是稀疏的。通常时域内的自然信号都是非稀疏的，但在某些变换域可能是稀疏的。不失一般性，考虑长度为N的离散信号f，记为f(n)，n=1，2，…，N。由信号理论可知，f能够用一组基ΨT=[ψ1，ψ2，…，ψm，…，ψN]的线性组合表示，则

其中，αk=＜x，ψk＞，α是N×1矩阵，Ψ是N×N矩阵。当信号f在基函数Ψ上仅有有限个非零系数时，称Ψ为信号f的稀疏基。

信号在稀疏基上仅有k个非零系数属于严格稀疏的情况，多数情况下信号无法满足严格稀疏的要求。但是，当信号的变换系数经过排序后可使指数级衰减趋近于零时，信号可以近似稀疏表示。

⇨测量编码

CS框架中，测量和编码是同时进行的，也就是说，可以直接获取压缩后的测量值。首先定义线性测量，对于一个待重构信号，它的线性测量可以用一个线性函数与它本身的内积来描述，对应表达式如下

其中，f(t)表示待重构信号，φi(t)表示第i个线性测量信号，yi表示第i个测量结果。可以用向量形式表示测量过程

其中，y为测量结果，Φ为测量矩阵，f为待重构信号。由于信号f可以用一组稀疏基函数进行展开，则测量过程可以表示为

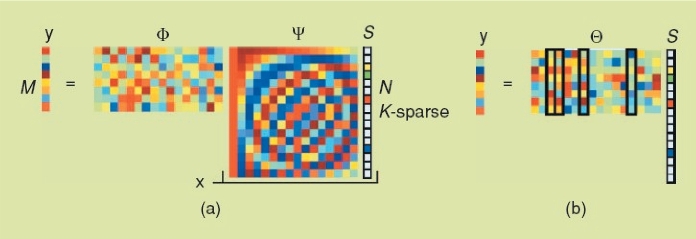
如图6-15所示，如果测量矩阵的维数是m×n，那么必须满足m＜＜n，否则一切将毫无意义。

(www.xing528.com)

图6-15 压缩传感测量矩阵示意图

⇨解码重构

CS框架中，当测量矩阵满足RIP准则时，我们就可以运用合适的重构算法正确地把未知信号准确恢复出来。重构信号最直接的方法就是通过求解l0-范数的最小化问题

直观上对式(6.4.5)的理解，可以解释为在满足方程y=Θs的无穷多个解中，找到一个最稀疏的解作为问题的最终解。

正交匹配追踪的算法流程如下：

第1步：初始化残差r0=y，增量矩阵Λ0为空矩阵，计数器t=1；

第2步：计算矩阵Θ的列向量Θi与残差值rt-1的内积，选择其中的最大值在矩阵Θ中所对应的列；

第3步：扩充增量矩阵，使Λt=[Λt-1，Θλt]，并删除矩阵Θ的第λt列；

第4步：用最小二乘法求解关于1×t维向量ut的方程Λtut=y；

第5步：重新计算残差值rt=y-Λtut，如果残差满足要求，则进入第7步，否则进入第6步；

第6步：使t=t+1，如果t≤k，返回第2步，否则进入第7步；

第7步：输出ut，则sλt=ut。