物理光学法简化散射分析及成像

由于成像的分析是在频域上进行的，因此，这里采用电磁散射分析中的频率方法计算目标的散射场，而时域和频域的回波也可以通过Fourier变换相互转换。物理光学(Physical Optics，PO)法是一种基于表面电流的方法，它从Stratton-Chu公式出发，引入物理上合理的高频假设：物体上某一点对该物体其他点的散射场的贡献和入射场相比是很小的，从而忽略了各个子散射单元之间的耦合作用，使得求解过程得到简化。根据物理光学近似条件和远场近似条件，求解远区散射场的物理光学法基本公式如下

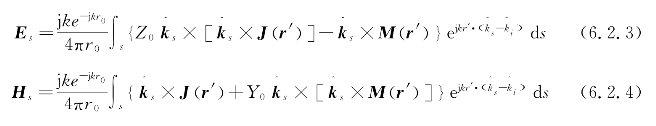
其中，r0为坐标原点到观察点的距离，r′为源点的位置矢量，k为波数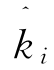，为电磁波入射方向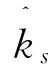，为电磁波散射方向，为入射面的外法相量，Z0为自由空间阻抗，Y0为自由空间导纳，J和M分别表示物体表面的等效感应电流和磁流。由于存在关系式因此，上述两个方程中的任何一个都可以用来计算远区散射场。对于金属目标，感应磁流为0，感应电流为

因此，远场散射可以简化为

物理光学法认为，目标被入射波照亮的部分会产生感应电流，电流的大小和强度由J=来计算；目标未被入射波照亮的部分电流为零。因此，整个目标分为两个区域：照明区和阴影区。物理光学方法首先要把散射体模型的阴影面和照明面分离出来，该过程就是面元遮挡判断。一个高效的自动遮挡判断算法既直接影响计算结果的精度，又可使计算过程更加快速。

为了能够进行遮挡的判断，先将遮挡判别分为单重遮挡和多重遮挡两类：如果某个面元仅仅是因为朝向，使得入射射线无法到达面元的外表面，从而被判断为阴影面，则称为该面元被单重遮挡；如果某个面元被判断为阴影面，其原因是他面元挡在该面元与入射波之间，则称该面元被多重遮挡。单重遮挡的判别比较简单，只需要利用面元的外法向量和入射波的方向矢量即可，如图6-1所示。

图6-1 单重遮挡示意图(www.xing528.com)

假设入射波的方向矢量为，面元的外法线为，则单重遮挡的判别公式为

单重遮挡判别的运算过程简单，运算速度快，计算时间也不多。

对于多重遮挡的判别，计算过程比单重遮挡要复杂，一般在单重遮挡识别后，再对剩余的照明面元进行处理。多重遮挡的示意图如图6-2所示，假定此时面元S1、S2、S3和S4在单重遮挡判别的过程中被识别为照明面，下面分析S3的多重遮挡判别过程。首先，从面元S3的中点引出一条射线，方向为入射波方向的反方向-，从而将问题转化为分析该射线与其余面元是否有交点。然后，依次判断该射线与各个面元是否有交点，如果有，则面元S3被判断为阴影面；反之，面元S3被判断为照明面。

图6-2 多重遮挡示意图

多重遮挡判断的运算量主要集中在通过几何关系求解射线与面元之间的交点。经过单重遮挡判断后，假设有N个照明面元，则多重遮挡的运算过程需要求解N 2次交点。对于电大尺寸目标，面元特别多，则多重遮挡过程就特别缓慢。为了加速这个过程，我们引入树型结构。首先，将目标区域按照空间位置进行分组(如图6-3所示)。其次，计算射线与面元的交点时，可以先计算射线与子区域的交点：若射线与某个子区域没有交点，则该子区域包含的所有面元都不会与该射线有交点；若射线与某个子区域有交点，则依次计算该区域包含的所有面元与该射线的交点。通过这种分组的策略，大大降低了射线与面元求交的过程，提高了计算效率。对于更大规模的问题，可以通过多层的树型结构来加速，其结构类似多层快速多极子中的树型结构，这里不再赘述。

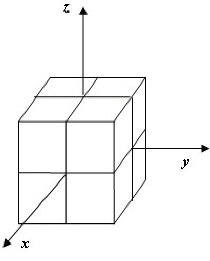
图6-3 目标区域的分组