在电磁散射数值分析中，矩量法是计算任意目标的散射的一种有效的工具。矩量法对积分方程进行离散，将其转化为对应的线性方程组Z n×n·I n×1=V n×1，其中，Z为阻抗矩阵，I为电流向量，V为入射场激励的右边向量，n为方程的未知量个数。一般情况下，矩量法产生的阻抗矩阵Z是一个稠密阵，矩阵中的每个元素都通过数值积分获得，使得计算阻抗元素的时间占整个散射计算求解时间的大部分。在宽频带散射分析中，随频率变化的RCS曲线往往变化剧烈，为了精确描述目标的频率变化特性，需要用较小的采样间隔在宽频带上不断重复地计算阻抗矩阵和求解方程，耗费大量的时间。
相对于诸如RCS此类随频率变化剧烈的物理量，阻抗矩阵元素随频率变化比较平缓。因此，采用阻抗矩阵插值的方法，可以减少阻抗矩阵填充的时间，从而节省宽频带散射计算的时间。对于三维散射问题，从电场积分方程(EFIE)和磁场积分方程(MFIE)的公式出发
可以看出，阻抗矩阵随频率的变化规律由格林函数决定。对于自由空间金属目标的散射，格林函数为
它是e的指数形式，随频率变化的趋势只跟波数k有关。阻抗矩阵元素可以近似地认为随着三维格林函数中的指数函数e-jkr而变化，即Zmn∝exp(-j kRmn)。此时定义
式(5.2.4)用于消除阻抗矩阵元素随频率变化的波动特性，使阻抗矩阵元素Z′mn在角宽的频带内较原来的阻抗矩阵元素Zmn变化得更平缓，从而使插值方法更加适合用于估计新的阻抗元素。
对于电大尺寸目标的散射问题，传统矩量法受到计算时间和内存的限制，无法进行有效的分析。快速多极子和多层快速多极子将阻抗矩阵分为远场和近场两部分
近场阻抗矩阵Znear用矩量法直接计算，远场阻抗矩阵Zfar用聚合、转移、配置因子隐式地表示，从而可以将矩量法的计算复杂度从O(N 2)降低到O(N log N)，内存消耗同样从O(N 2)减低到O(N log N)。在利用矩量法结合多层快速多极子分析宽频带电磁散射问题时，由于远场阻抗矩阵的聚合、转移、配置因子构造时间少、存储消耗少，因此主要的计算开销集中在近场阻抗矩阵填充和线性方程组求解，因此，同样可以利用插值技术加速近场阻抗矩阵的填充，从而提高宽频带电磁散射分析的效率。
插值函数采用有理函数
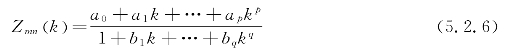(www.xing528.com)
其中，Zmn为阻抗矩阵中第m行和第n列元素，k为波数，a0，a1，…，ap和b1，b2，…，bq为插值系数，可以通过下面的方程求得
利用有理函数插值，可以用很少的采样点获得宽频带的RCS响应。
为了分析阻抗矩阵插值的效果，我们分析了导弹(未知量7818)、金属平板(1m×1m，未知量34 165)、金属立方体(1m×1m×1m，未知量121 854)的计算结果(如图5-1、图5-2、图5-3所示)。第一个例子的入射角度为θ=90°、φ=45°，第二、三个例子的入射角度为θ=0°、φ=45°。迭代求解采用的是重启的GMRES算法，子空间维数为30，迭代收敛的精度为10-3。所有的算例都是在PC机上仿真，CPU为Intel Core II 8300 2.66GHz，内存为1.96 GHz。从扫频的RCS曲线可以看出，阻抗矩阵插值的曲线明显比电流插值的曲线要准确，因此，可以证明阻抗矩阵随频率变化的趋势较电流随频率变化的趋势更加平缓。然而，从计算时间上来看，阻抗矩阵插值的计算时间跟电流插值的计算时间相比，没有任何优势，甚至花费的计算时间更长(如表5-1所示)。其主要原因为：阻抗矩阵构造的时间虽然缩短了，但迭代求解的时间没有改变。对于性态比较差的方程，迭代法收敛非常慢，使得求解的时间远远大于阻抗矩阵构造的时间。在这种情况下，即使阻抗矩阵构造的时间能够大幅度降低，计算需要花费的总时间仍然很多。因此，对性态较差的方程组，仅仅使用阻抗矩阵插值的方法，计算效率得不到很大的改善，需要采用新的方法对阻抗矩阵插值进行改进。
图5-1 导弹的计算结果：VV极化的RCS扫频曲线
图5-2 金属平板的计算结果：VV极化的RCS扫频曲线
图5-3 金属立方体的计算结果：VV极化的RCS扫频曲线
表5-1 频率扫描的总时间比较(时间：s)
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
