利用本节算法,可以避免逐点计算带来的计算时间的负担,又可以避免采样点的选择,从而可以灵活快速地分析任意目标的二维单站RCS。下面利用几个数值算例来说明该方法的效果。入射波选择为平面波,扫描范围均为俯仰角0°~180°和方位角0°~180°,扫描间隔为1°。由于右边向量个数非常多,因此,这里采用两种策略来减轻直接进行SVD的负担。第一种策略是用多层SVD方法,第二种策略是采用自适应采样技术和ACA混合的方法。当采用多层SVD时,所有算例中,将右边向量均匀分成181个子矩阵,每个子矩阵包含181个右边向量,分别对每个子矩阵进行奇异值分解,然后进行合并,再对合并后的特征向量进行奇异值分解,获得整个右边矩阵的特征向量。
下面通过分析NASA Almond、Ogive、Double-Ogive的单站RCS,未知量分别为1815、2571和4635,给出了改进算法计算的RCS精度(如图4-8、图4-9、图4-10所示)。考虑到此时右边向量的个数为32 761,IMSL中的库函数对这种规模的SVD分解已经不能分析,且多层SVD同自适应采样ACA结果几乎一样,因此,算例中的RCS结果只列出自适应采样ACA的计算结果,计算时间则通过表格对比多层SVD和自适应采样ACA的时间。
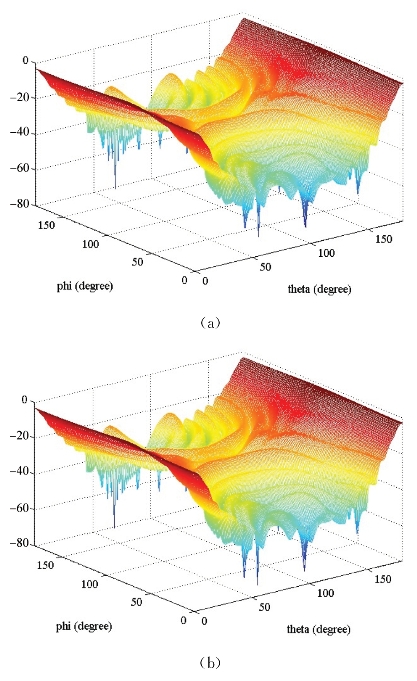
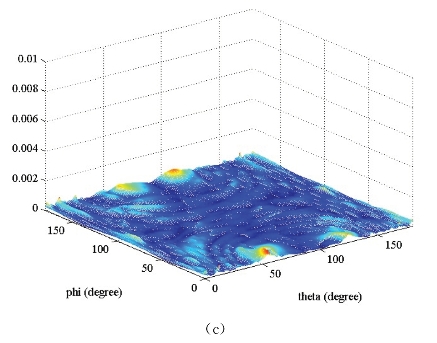
图4-8 NASA Almond单站散射,频率5 GHz,θθ极化,俯仰角0°~180°,方位角0°~180°
(a)直接计算结果;(b)多层SVD计算结果;(c)多层SVD相对误差
通过RCS的对比,可以看出直接计算和本节快速算法的结果几乎一样,为了更加准确地说明自适应采样的精度,在RCS结果图之后还给出了相对误差的二维图。相对误差均保持在0.2%之内,误差要优于第3章提出的自适应采样算法。其原因是:在本节算法中,对右边向量进行自适应采样的过程中,程序终止条件的要求比较高,稍微多选择一些右边向量对整个计算时间的影响不大,但对精度的影响就很明显。

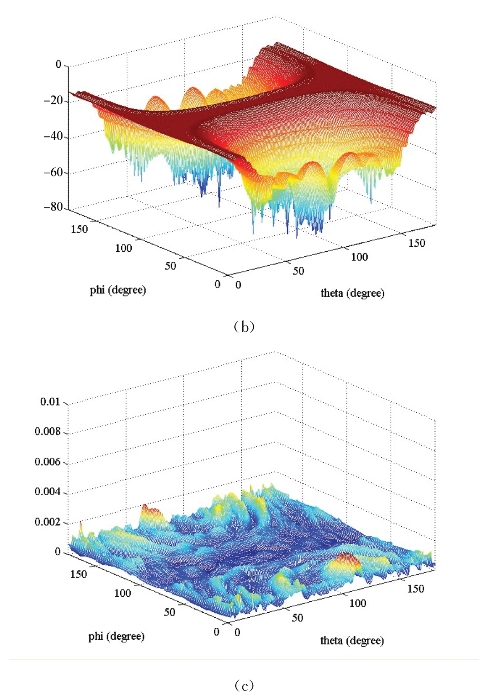
图4-9 金属Ogive单站散射,频率8 GHz,θθ极化,俯仰角0°~180°,方位角0°~180°
(a)直接计算结果;(b)多层SVD计算结果;(c)多层SVD相对误差(https://www.xing528.com)
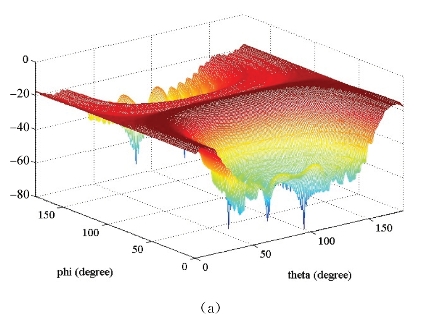
图4-10 金属Double-Ogive单站散射,频率12 GHz,θθ极化,俯仰角0°~180°,方位角0°~180°
(a)直接计算结果;(b)多层SVD计算结果;(c)多层SVD相对误差
与第3章的相对误差定义一样,所有算例中,相对误差定义为

其中,Eapprox为利用本节方法估计的散射场,Edirect为直接求解方程得到的精确的散射场,|Edirect|max表示直接计算得到的散射场中的最大值。从插值结果和相对误差可以看出,多层SVD算法和自适应插值算法都可以准确地获取任意目标的二维RCS扫描结果,两种方法的误差几乎是一样,其根本原因是这两种方法的核心思想都是基于SVD分解的方法。下面给出两种改进的低秩分解计算时间的分析。从计算时间的比较可以发现,两种改进策略均比直接SVD分解需要的时间要少。将这两种改进方法进行比较可得,自适应采样结合ACA的方法在计算效率上的改善更加明显,能够极大地降低单站RCS扫描的计算时间。
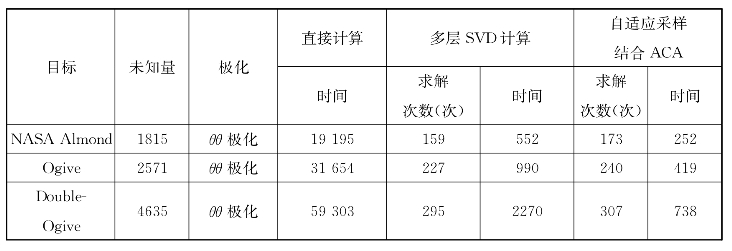
表4-2 算例NASA Almond,Ogive和Double-Ogive插值计算与非插值计算时间的对比(时间:s)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




