ACA技术在宽频带宽角度电磁散射分析及成像中的应用

利用多激励向量的低秩特性加速单站RCS的计算，核心的操作是对多个右边向量进行奇异值分解。为了能够快速地进行奇异值分解，前面分别采用了多层SVD和自适应采样技术，其本质思想是尽量降低进行奇异值分解的矩阵的维数，从而能够有效地加快SVD的进程。我们都知道，进行奇异值分解的目的是获取矩阵的低秩表示，由此可知矩阵都是低秩的，因此，本节我们考虑能否再次利用这种低秩特性来加速奇异值分解。

自适应交叉近似(ACA)算法可以利用矩阵的低秩特性，快速近似地获取矩阵的低秩分解形式[98-99]。根据SVD的定义，对于任何一个低秩的矩阵A，可以表示成三个矩阵相乘的形式

其中，∑k为对角阵表示A的特征值，酉矩阵Uk和酉矩阵Vk为A的特征向量，上标H表示共轭转置，k为矩阵A的秩。用图4-7表示如下

图4-7 低秩矩阵ACA分解示意图

ACA的基本思想为：一个矩阵的低秩表示形式可以通过矩阵的若干行和若干列的元素来快速获得，而不需要矩阵的所有元素。也就是说，通过合适的选行和选列，就可以近似获得矩阵的奇异值分解的形式，从而达到提高运算效率的目的。这里要注意，ACA能够提高SVD效率的前提为矩阵是低秩的。

下面给出ACA的具体算法流程：

令UACA=NULL用来存储选择的列向量，令VACA=NULL用来存储行向量。(www.xing528.com)

1.随机选择第一列u1，并令UACA=UACA∪{u1}，寻找u1中的最大值u1k，然后选择u1k所对应的行为第一行v1，并令VACA=VACA∪{v1}；

2.寻找vi中的最大值vik，然后选择vik所在的列为第i+1列ui+1；

3.计算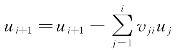，并令UACA=UACA∪{ui+1}；

4.同样寻找ui+1中的最大值ui+1，k，然后选择ui+1，k所对应的行为第i+1行vi+1；

5.计算，并令VACA=VACA∪{vi+1}；

6.判断当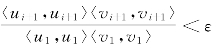时，算法停止，此时的UACA和UACA就是我们所需要的矩阵的低秩分解，否则转到第2步继续执行。

经过ACA的操作，矩阵的低秩分解形式为A=UACA·VACA H。在整个执行过程中，ε的选择非常重要。如果选择太小，则增加不必要的计算负担；如果选择太大，则精度得不到保证。在本书中，我们同样选择ε=10-3。由于ACA代替了传统的SVD，因此，ACA可以与自适应采样技术直接相结合，从而得到新的改进算法。