多激励向量低秩分解：快速分析和成像

利用积分方程求解三维目标的电磁散射问题可以简单描述为对线性方程组的求解，目标被平面三角形贴片离散之后，表面电流用RWG基函数模拟，并对表面积分方程实施Galerkin测试，从而形成线性方程组为

其中，A为阻抗矩阵，x为RWG基函数的系数，b为目标表面的入射场经测试后形成的右边向量。通过求解该线性方程组，得到RWG基函数的系数，便可以计算任意理想导体目标的散射问题。

单站RCS的计算，则对应为求解多个右边向量的方程组，描述如下

其中，A为阻抗矩阵，x为电流向量，b为右边向量。写成矩阵形式如下

其中，X=[x(θ1)，x(θ2)，…，x(θn)]，B=[b(θ1)，b(θ2)，…，b(θn)]。直接对方程求解，求逆的次数为n，当n很大时，逐次求解将会造成巨大的计算负担。

如图4-1所示，对右边矩阵B做奇异值分解(SVD)，方程可以转化为

其中，B=U·∑·V H，∑为对角阵表示B的特征值，酉矩阵U和酉矩阵V为B的特征向量，上标H表示共轭转置。由于相邻电流之间具有相关性，使得矩阵B具有低秩特性，因此，B可以通过矩阵的奇异值分解进行压缩。将B的SVD形式去掉小特征值和对应的特征向量，可以近似地表示为

其中，矩阵Uk、∑k和Vk分别表示U、∑和V保留k个最大特征值分量的结果，可以证明，Bk与B近似相等。于是，方程组可以进一步表示为

从而得到方程的解X为

从上面的式子可以看出，方程求逆的操作全部集中在计算A-1·Uk，求逆的次数为k，因此可以得出，在损失很少的精度的前提下，求解方程的次数可以从n次降到k次。一般情况下，当n很大时，k满足k≪n。

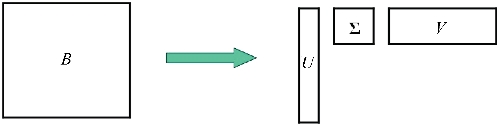
图4-1 多右边向量的低秩分解

该算法最关键的一步是k的选取，k太大会造成计算量的增加，k太小会使得结果不准确。假定矩阵B的最大特征值是λmax，且特征值按从大到小排列为λ1＞λ2＞…＞λn。我们初步给出k的一个选择方案，即k的值使得

特征值λk+1，λk+2，…，λn和对应的特征向量将从矩阵的分解形式中删除，来获得矩阵的低秩表示。为了说明这种选取方式的稳定性，对于k的选取，我们用算例来简要分析一下当ε选取不同的值时，计算时间和精度的变化(如图4-2所示)。(www.xing528.com)

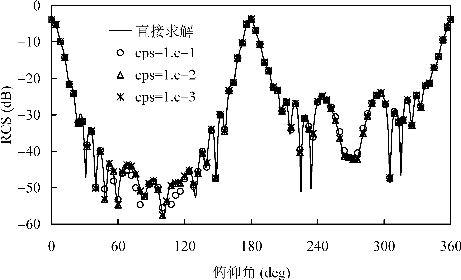
图4-2 截断标准不同时，Almond的单站RCS曲线

其中当ε=10-1时，主特征值k的数值为21，即方程求解21次，计算总时间为26秒；当ε=10-2时，主特征值k的数值为25，即方程求解25次，计算总时间为30秒；当ε=10-3时，主特征值k的数值为29，即方程求解29次，计算总时间为35秒。当ε=10-1时，图中存在

很明显的误差，而对于ε=10-2或10-3时，很难看出这两种选取方式的结果与直接计算的结果有明显不同，可见当ε=10-2时只有很小的误差且已经能够满足计算的需求。但是，为了程序的稳定性，我们采用更加苛刻一点的条件，因此，后面的数值算例均用ε=10-3这个准则。

根据我们提出的基于SVD的单站RCS快速算法，我们分析了NASA Almond、Ogive和Double-Ogive的单站RCS，未知量分别为1815、2571和4635。下面给出了直接计算和采用SVD算法计算的RCS曲线比较(如图4-3、图4-4、图4-5所示)。从结果中可以看出，基于SVD的算法可以准确地逼近原始曲线。

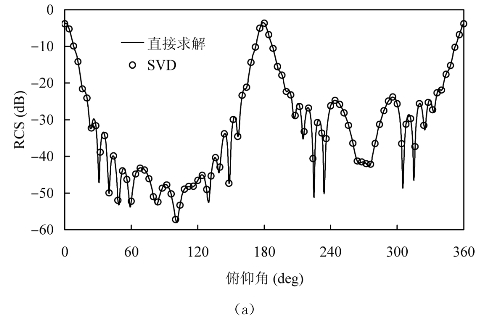
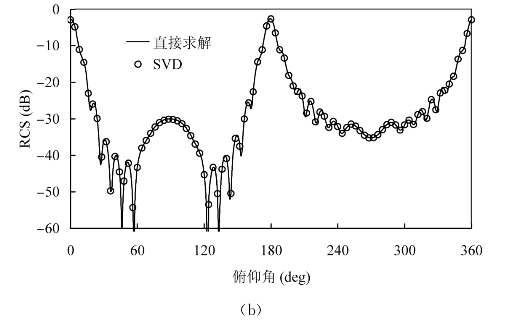
图4-3 NASA Almond单站散射，频率5 GHz，俯仰角0°～360°，方位角0°

(a)θθ极化的RCS曲线；(b)φφ极化的RCS曲线

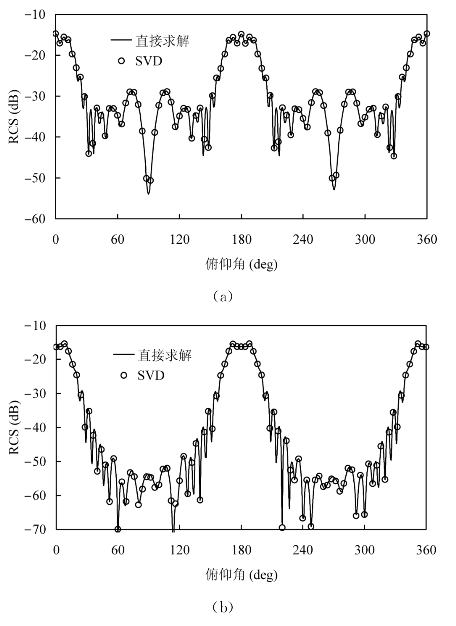
图4-4 金属Ogive单站散射，频率8 GHz，俯仰角0°～360°，方位角0°

(a)θθ极化的RCS曲线；(b)φφ极化的RCS曲线

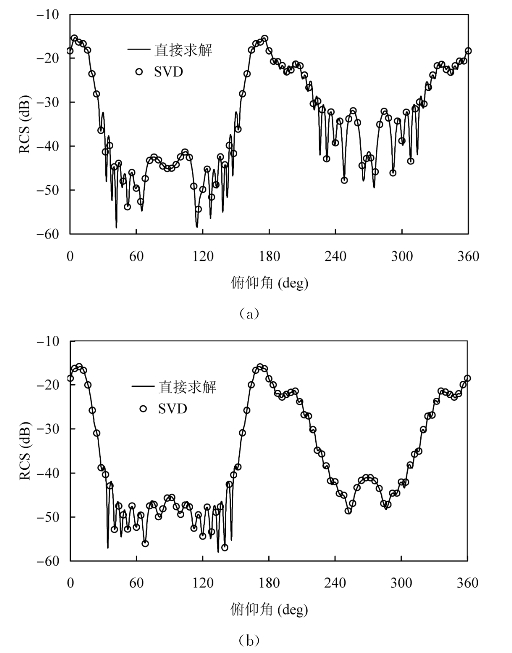
图4-5 金属Double-Ogive单站散射，频率12 GHz，俯仰角0°～360°，方位角0°

(a)θθ极化的RCS曲线；(b)φφ极化的RCS曲线

表4-1给出了选择的特征值的个数，以及直接计算和快速方法的计算时间对比，数值算例均在PC机上完成，CPU为Intel(R)Core(TM)2 6300 1.86 GHz，内存为1.96 GB。从中可以看出，快速算法可以根据入射场的低秩特性，自动地选择特征值个数，使计算程序的效率、稳定性和灵活性得到提高。

表4-1 直接计算与SVD计算的对比

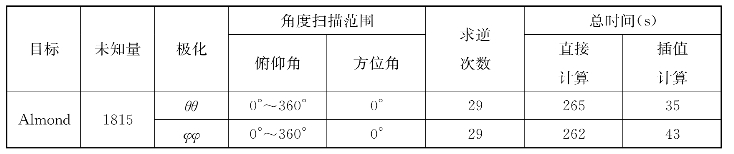
续表