AWE外推技术在宽频段电磁散射分析中的应用

渐近波形估计技术在电磁领域的应用始于20世纪90年代，最初用于静态电磁场分析，如微波器件宽带频域响应的快速计算。20世纪90年代后期，渐近波形估计被逐渐应用到电磁场的全波分析中，如目标散射的快速计算。本节主要阐述渐近波形估计技术快速计算宽角度雷达散射截面的基本原理，包括渐近波形估计外推算法、渐近波形估计分段插值算法和渐近波形估计与样条的结合。

分析导体目标的宽角度单站散射，本质上是求解MoM形成的线性方程组在每个角度上的电流系数I，方程如下

其中，Z为阻抗矩阵，I为待求的电流系数，V为入射平面波产生的右边激励向量，θ和φ分别是俯仰角和方位角。在这里，右边向量V是角度θ和φ的连续函数，阻抗矩阵Z则始终不变。因此，电流系数I也可以写成角度θ和φ的连续函数，如下

为了简单起见，我们首先分析一维情形。不失一般性，这里分析对俯仰角θ的快速扫描，即

对I(θ)在θ0处进行Taylor展开，得到展开式

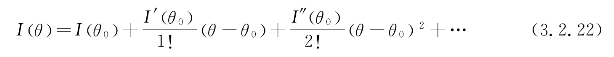
为了能够用Taylor级数正确地表达表面的电流分布，需要足够多的展开项，因此，必须在展开点θ0处计算足够高次的导数I(n)(θ0)，其中n=1，2，3，…。Taylor级数受到收敛半径小、精度有限的制约，使得n必须非常大才能准确逼近宽角度的电流系数。当n逐渐增大时，Taylor级数又会产生严重的Runge现象(龙格现象)。因此，需要新的技术对Taylor级数加以改进。

AWE采用有理函数式来表示Taylor级数展开，即利用Taylor级数来获得有理函数式的系数，然后用有理函数式进行外推，从而获得比Taylor级数更宽的收敛半径。电流向量用有理函数式展开为

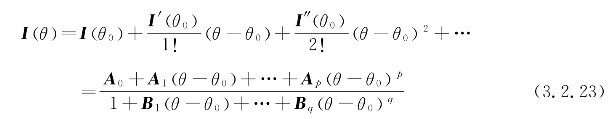
其中，p和q为有理函数式的阶数，且满足，系数A0，A1，…，Ap和B0，B1，…，Bq通过求解方程得到。在利用AWE对电流外推的过程中，由于电流向量中各个元素之间没有相关性，可将上式写成标量形式(www.xing528.com)

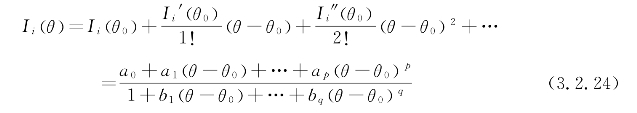
其中，Ii表示电流向量中的第i个元素，而该元素对应的系数a0，a1，…，ap和b0，b1，…，bq可通过求解如下方程组得到

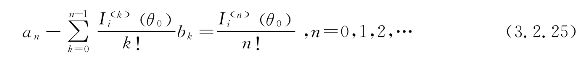
综上所述，只要求得参考点θ0处的高次导数值，就可以利用有理函数式快速获得目标的宽角度RCS。

下面利用NASA Almond的单站散射RCS曲线来比较Taylor级数和AWE的收敛半径。入射波的频率为5GHz，单站扫角的范围为150°～210°，参考点取中点180°。在这里考察展开阶数为6和10两种情况，图3-1和图3-2中的结果分别对应阶数为6和阶数为10的外推RCS曲线。根据两幅图的结果，发现极化对收敛半径的影响不大。当阶数为6时，Taylor级数的收敛半径为20°，而AWE的收敛半径为30°；当阶数为10时，Taylor级数的收敛半径为30°，而AWE的收敛半径可达50°。因此，根据参考点的高阶导数信息，利用AWE外推算法可以获得比Taylor级数所获得的信息更宽。

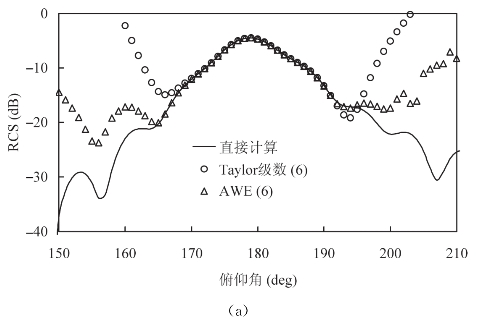
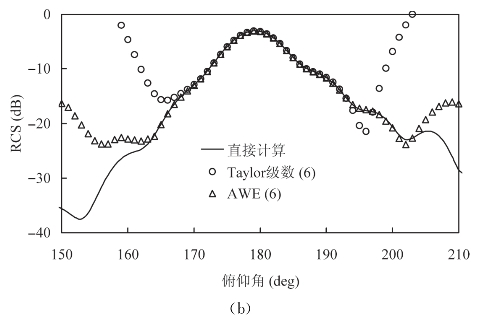
图3-1 NASA Almond单站散射，频率5GHz，俯仰角150°～210°，方位角0°，外推展开的阶数为6

(a)θθ极化的RCS曲线；(b)φφ极化的RCS曲线

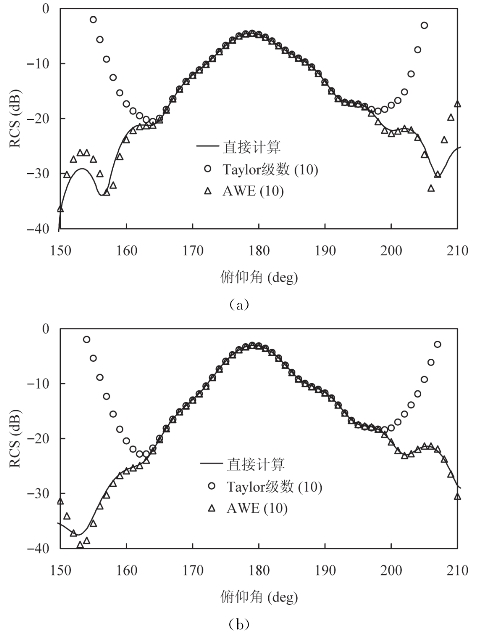
图3-2 NASA Almond单站散射，频率5GHz，俯仰角150°～210°，方位角0°，外推展开的阶数为10

(a)θθ极化的RCS曲线；(b)φφ极化的RCS曲线