宽频带宽角度电磁散射计算及成像

在利用插值方法快速计算单站雷达散射截面时，往往需要用到插值函数的导数值，在论述具体的插值方法之前，先给出电流的导数值的计算公式。

混合场积分方程经过矩量法离散，形成的线性方程组为

其中，Z为阻抗矩阵，I为RWG基函数的系数，V为目标表面的入射场经测试后形成的右边向量。具体表达式如下

在求解单站RCS的过程中，阻抗矩阵Z是不随入射角度变化而变化的，因此，未知量I为右边向量V的函数，且I的n阶导数可以表示为

可见，要求得I的导数，就必须先求得V的导数，然后通过求解线性方程组来获得。

根据V的表达式，我们发现V是俯仰角θ和方位角φ的二元函数，即

以计算俯仰角的导数为例，可以直接写出右边向量对俯仰角θ的导数为

V导数的计算的关键部分在于对入射电场和入射磁场的导数进行准确计算。入射电场和入射磁场形式为(www.xing528.com)

其中，表示的电场和磁场的方向，同样为俯仰角θ和方位角φ的二元函数。入射电场和入射磁场的导数的表达式为

其中，u和v的表达式为

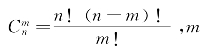=0，1，2，…，n表示的是二项式的展开系数。对于方位角方向的导数值，可以用相似的步骤进行推导。

对于的导数值，与极化方式有关，这里我们只考虑线极化，假定极化角度为γ，那么的表达式为

于是对俯仰角θ的导数值的表达式为

对方位角φ的导数值的表达式为

求得了右边向量V的导数值之后，便可以通过解方程的过程求得未知量I的导数，其计算复杂度等同于求解未知量I的计算复杂度。可见，如果能够在插值过程中避免导数值的计算，是可以节省运算量的。