快速求解线性方程组-宽频带宽角度电磁散射快速分析及成像

当计算电大尺寸目标电磁散射问题时，未知量比较大，传统的直接解法受到时间和内存的限制，无法有效地进行求解。当采用多层快速多极子加速矩阵矢量乘的操作之后，大家普遍采用的求解方法是迭代求解器，如共轭梯度法和广义最小余量法等。本书采用广义最小余量法及其改进的方法求解大型线性方程组，下面介绍这种方法的基本原理。

设所求线性方程组为Ax=b，其中，A为一非奇异矩阵，b∈Rn为一给定向量。令x=x0+z，则原方程等价于

其中，r0=b-Ax0。记km和Lm是Rn中两个m维子空间，分别由张成。GMRES的基本思想为：在子空间km中寻找方程Az=r0的近似解zm，使得残余向量r0-Azm和Lm中所有向量正交。

首先取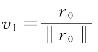，然后对于k=1，2，…，m，计算

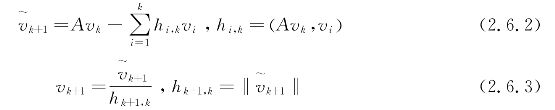
在这个过程中，只要hk+1，k≠0，当k=m时，我们就得到一组向量其中量 是Span{r0，Ar0，…，A m-1r0}中的一组标准正交基，且vm+1⊥Span{r0，Ar0，…，A m-1r0}。

Arnoldi过程可以改写为

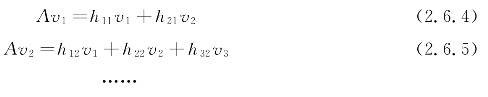
用矩阵符号统一写为

其中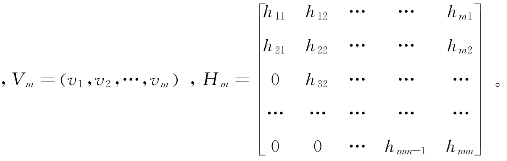两边均左乘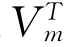，由正交的性质，可得

根据r0=AVmym，两边右乘ym，得

由于

则

(www.xing528.com)

只要解出ym，就可以求出近似解zm。

算法流程：

Step 1：给定初值x0，将方程化为Az=r0。

Step 2：对于m=l(l=1，2，…)，由Arnoldi过程求出及Hm。

Step 3：如果Hm为奇异阵，则算法中断，更换x0转向step 1；否则，求解Hmym=βe1得ym，并计算zm=Vmym。

Step 4：若‖r0-Azm‖＜ε，则取x*=x0+zm，算法结束；否则，取l=l+1，转向Step 2。

对于方程Az=r0，对于固定整数值m，取Lm=AKm，即Km=Span{ r0，Ar0，…，A m-1r0}和Lm=Span{ Ar0，A 2r0，…，A mr0}，利用Galerkin原理，在空间Km中寻找近似解zm，使残余向量rm=r0-Azm的2-范数，在所有Km中的向量中达到极少。

算法流程：

Step 1：选择x0∈Rn，计算；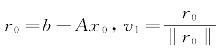

Step 2：对于m=l(l=1，2，…)，调用Arnoldi过程，得到和；

Step 3：求解得到ym；

Step 4：计算zm=Vmym；

Step 5：若‖r0-Azm‖＜ε，则取x*=x0+zm，算法结束；否则，取l=l+1，转向Step 2。

下面给出利用矩量法和多层快速多极子计算目标RCS的算例，数值算例在计算机上完成，CPU(中央处理器)为Intel(R)Core(TM)2 6300 1.86 GHz，内存为1.96 GB。结构为金属球，半径为1 m，入射平面波频率为6 GHz，树型结构分为6层，最细层分组的大小为0.3波长(0.015 m)，最细层非空组个数为67 015，采用重启的GMRES求解，子空间维数为30，其θθ极化的双站RCS曲线和收敛曲线如图2-4所示。整个计算过程耗时6767秒，内存开销为1.2 GB。

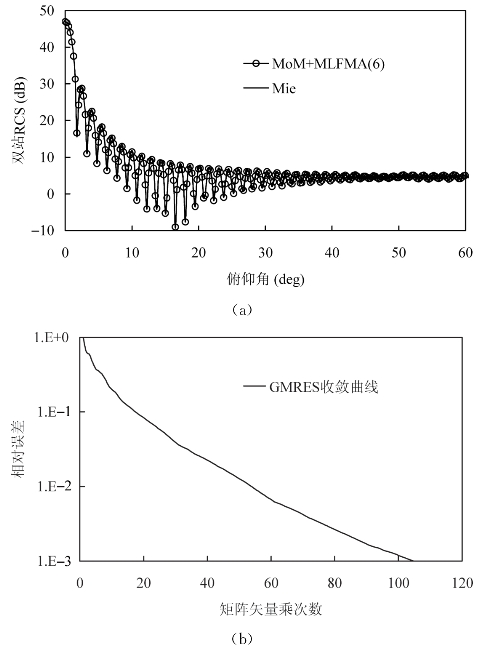
图2-4 金属球

(a)双站RCS曲线；(b)GMRES收敛曲线