宽频带宽角度电磁散射快速分析及成像-快速多极子方法

快速多极子[35-37]和多层快速多极子方法[38-40]是当今最令人瞩目的积分方程数值算法，具有精度可控和高效率的优点，被广泛应用于各种复杂目标的电磁散射分析，并且被美国计算物理学会评为20世纪十大算法之一[41]。

快速多极子方法的数学基础是矢量加法定理，即利用加法定理对积分方程中的格林函数进行处理，通过在角谱空间中展开，利用平面波进行算子对角化，最终将稠密阵与矢量的相乘计算转化为几个稀疏阵与该矢量的相乘计算。其基本原理为：将散射体表面上离散得到的子散射体分组，任意两个子散射体间的互耦根据它们所在组的位置关系而采用不同的方法计算。当场点和源点处于近邻组时，耦合作用采用传统的矩量法直接计算；而当它们处于非近邻组时，则采用聚合、转移和配置三步进行计算，实现场点和源点的分离。对于一个给定的场点组，首先，将它的各个非相邻组内所有子散射体产生的贡献“聚合”到各自的组中心进行表达；其次，将这些组的贡献由这些组的组中心“转移”至给定场点组的组中心进行表达；最后，将得到的所有非相邻组的贡献由该组中心“配置”到该组内各子散射体(如图2-2所示)。对于散射体表面上的N个子散射体，直接计算它们的互耦时，每个子散射体都是一个散射中心，即为一个单极子，共需数值计算量为O(N 2)。应用这种快速多极子方法，任意两个子散射体的互耦由它们所在组的组中心联系。各个组中心就是一个多极子，其数值计算量为O(N 1.5)。对于源点组来说，该组中心代表了组内所有子散射体在其非相邻组产生的贡献；对场点组来说，该组中心代表了来自该组的所有非相邻组的贡献，从而减少了散射中心的数目。

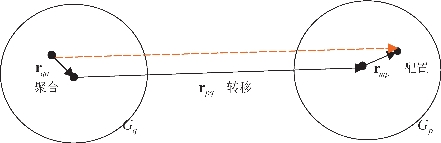
图2-2 将两元素的直接作用分解成三部分：聚合、转移、配置

对于电大尺寸目标的散射，其未知量数目N≫1，此时应用多层快速多极子方法将获得比快速多极子方法更高的效率。多层快速多极子方法是快速多极子方法在多层级结构中的推广。对于N体互耦，多层快速多极子方法采用多层分组计算，即对于附近区强耦合量直接计算，对于非附近区耦合量则用多层快速多极子方法实现。多层快速多极子方法基于树形结构计算，其特点是：逐层聚合、逐层转移、逐层配置、嵌套递推。对于二维情况，它将求解区域用一正方形包围，然后再细分为4个子正方形，该层记为第一层；将每个子正方形再细分为4个更小的子正方形，则得到第二层，此时共有42个正方形；依次类推得到更高层(如图2-3所示)。对于三维情况，则用一正方体包围，第一层得到8个子正方体。随着层数增加，每个子正方体再细分为8个更小的子正方体。显然，对于二维、三维情况，第i层子正方形和子正方体的数目分别为4i，8i。对于散射问题，最高层的每个正方形或正方体的边长为半个波长左右，由此可以确定求解一个给定尺寸的目标散射时多层快速多极子方法所需的层数。由于每层数值计算量均为O(N)量级，共有log N层，所以多层快速多极子方法计算矩阵与矢量相乘的工作量为O(N log N)量级，内存需求也为O(N log N)量级。

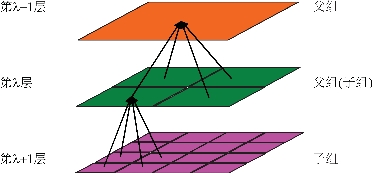
图2-3 二维多层快速多极子方法中的分层结构

下面给出具体公式。由加法定理可知，自由空间的格林函数可以展开为

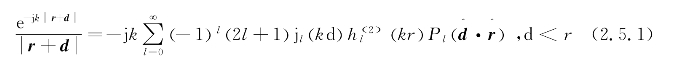
其中，jl(k d)为第一类l阶球Bessel函数，hl(2)为第二类l阶球Hankel函数，为l阶Legendre多项式。由等式

则格林函数可以进一步表示为

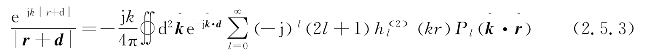
其中(www.xing528.com)

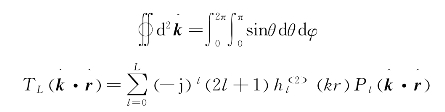
上式中，L为无穷求和的截断项数，在图2-2中，对于场点rm和源点rn，有

由于在远区组间，满足|rpq|＞|rmp+rnq|，则

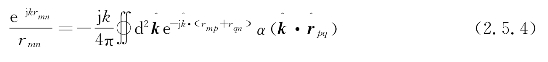
其中

于是，CFIE中的矩阵矢量乘操作可以表示为

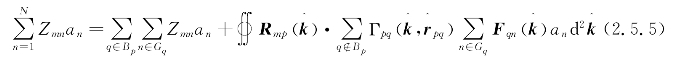
其中

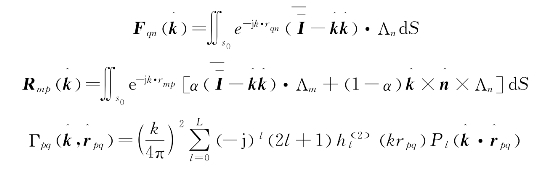
式(2.5.5)中Bp代表来自附近组的贡献，分别为聚合因子和配置因子。由于聚合和配置因子只与球坐标中的θ和φ有关，因此又称为辐射方向图和接收方向图。