RWG基函数和Galerkin测试

当采用矩量法分析导体目标的表面积分方程时，对于任意形状物体，其表面均可以采用平面三角形贴片来模拟，表面的电流则采用平面RWG基函数[34]，其数学表达式为

其中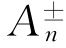，表示相应三角形的面积，ln为边长，各符号定义如图2-1所示。

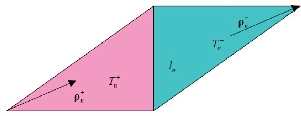
图2-1 平面RWG基函数示意图

RWG基函数具有两个重要特性：第一个特性是棱边法向分量的连续性，它保证了电流横跨公共边时的连续；第二个特性是两个三角形的基函数散度大小相等、符号相反，该特性保证了与基函数对应的电荷的总和为0。

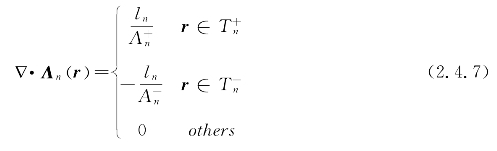
矩量法中测试函数的选取是多样的，较为常用的检验方法包括点匹配法和Galerkin法。点匹配就是选择δ函数作为测试函数，此时积分方程中的积分形式非常简单，并且计算过程最为简单。Galerkin测试就是选择基函数作为测试函数进行检验计算。点匹配过程最为简单，然而计算效果具有一定的局限性，Galerkin测试过程虽然烦琐，却最为稳定。当采用RWG函数作为基函数时，Galerkin测试过程被用于表面积分方程的求解。

目标被平面三角形贴片离散之后，表面电流用RWG基函数模拟，并对CFIE实施Galerkin测试，从而形成线性方程组

(www.xing528.com)

其中，Z为阻抗矩阵，I为RWG基函数的系数，V为目标表面的入射场经测试后形成的右边向量。具体表达式如下

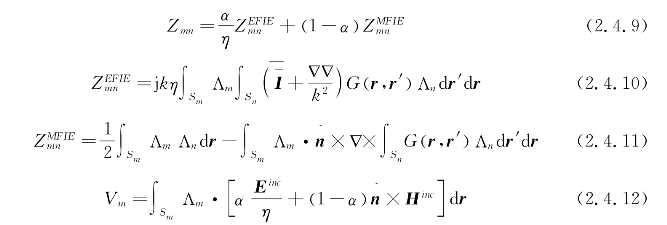
通过求解该线性方程组，得到RWG基函数的系数，便可以计算任意理想导体目标的散射问题。

对于远区散射，格林函数可以近似地表示为

因此，远区散射场的表达式可以简化，从而得到远区散射场的表达式如下

获得远区散射场后，就可以用下面的公式计算目标的雷达散射截面