基于词汇功能的研究点推荐方法及相似度计算

记现有的学术文献中已经出现过的问题及方法分别为（t1，t2，…，tk）和（m1，m2，…，mn），即现有的研究中已经出现了k种问题以及n种方法，方法和问题之间是多对多的关系，假设问题ti的解决方法的集合为Mi，方法mi能够解决的问题集合为Ti。问题及方法的关系构成二部图G，如图6-9所示。图中问题及方法使用直线相连，实线表示连接的问题和方法构成了问题方法对，也即该方法能够用于解决该问题，虚线表示连接的方法还没有应用于解决连接另一端的问题。

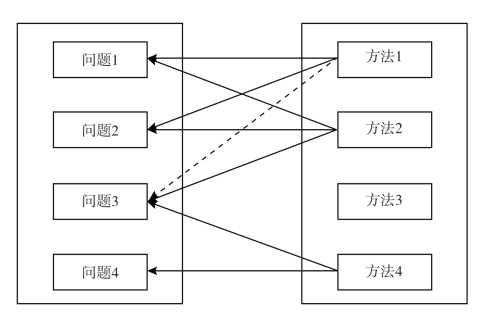
图6-9　问题与方法二部图（包含潜在关联关系）

本节接下来借鉴协同推荐的思想提出一个基于词汇功能的研究点推荐方法。

6.1.2节给出了两个假设：

第一，问题相似度可以通过使用的方法进行衡量；方法相似度可以通过其解决的问题进行衡量。如果两个问题（方法）对应的方法（问题）集合的交集越大，那么两个问题（方法）越相似。

第二，问题越相似，越有可能使用同一方法加以解决；方法越相似，越能够解决同一类问题。(www.xing528.com)

第一个假设给出了问题与问题、方法与方法之间如何度量相似性的问题。按照这一假设，在图6-9中，问题1可以使用方法1和方法2加以解决，因此可以将问题1表示为一个集合，集合包括方法1和方法2；同理，问题2也有着同样的表示；问题3能够使用方法2和方法4解决，则问题3可以表示为方法2和方法4组成的集合。

第二个假设给出了研究点推荐的工作原理。在图6-9中，由于方法1和方法2具有较高的相似性，因此，方法1也有可能能够用于解决问题3。

为了度量问题与问题、方法与方法的相似度，本书中使用Jaccard系数进行集合间的相似性计算。

为了给定问题推荐方法，或者给定方法推荐问题，这里使用了一个简单的策略。以方法为例，当为方法m推荐可解决的问题时，首先找到该方法相似的方法M，也即Jaccard系数计算得到的相似度不为0的方法，对这些方法涉及的所有问题Q，对每一个问题q∈Q，q的得分score（q，m）为：

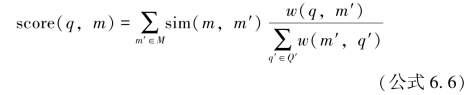
其中，sim（m，m′）表示方法m与方法m′之间的相似度，w（q，m′）表示m′和q之间的权重，通常为两者作为问题方法度的频次，但本节里，这个值设为1，Q′表示方法m′关联的所有问题集合。