微观形貌测量技术：二维非权重模型

假定Φij 为二维离散点上的去包裹相位，ϕij 为对应的包裹相位，则有

原理如下：寻找已解包裹的相邻像素点间相位差值与该相邻像素点间包裹相位差值之差的最小二乘解，即在理论上解包裹相位差应当等于包裹相位差，而实际由于解包裹的不正确性，两者间有差值存在。

定义包裹算子W，有

定义包裹相位差

式中，上标x 和y 分别指行相位差及列相位差。

作最小二乘

求解S 最小二乘意义下的解Φij即可获得相位解包裹的解。

Hunt 的矩阵公式给出了上述最小二乘矩阵的法方程，即

式（4−37）为包裹相位差与去包裹相位差的关系。对其作简单恒等变换，得

式中

实际上，式（4−36）是M × N 矩形网格上的离散Poisson 方程

式（4−40）对所有矩形网格点i=0，1，2，…，M−1； j=0，1，2，…，N–1 都是有效的，并且被用于计算ρij的相位差仅在网络区域内是非零的。这个限制源自最小二乘公式，因此可以直接得出离散Poisson 方程的Neumann 边界条件。

由此看出，相位解包裹问题的最小二乘解在数学上等于M × N 矩形网格上具有Neumann 边界条件的离散Poisson 方程解。下面引入快速离散余弦变换（DCT）来求解。(www.xing528.com)

二维离散余弦变换对如下：

DCT 正变换：

DCT 反变换：

Cmn为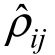的二维DCT 谱值，即在DCT 域的精确解。余弦展开自动地加有Neumann 边界条件，∇Φ·n=0，从而给出了如下所示相位的精确解：

展开Φij，得

将式（4−44）代入式（4−46），并在式（4−46）右边作类似的展开，化简整理后，即得Φij在DCT 域的精确解：

对该式进行DCT 反变换即可得到相位解包裹后的Φij。式（4−38）自动地加有Neumann 边界条件：

将二维非权重相位解包裹算法归结如下：

（1）对由式（4−38）计算得到的阵列ρij进行式（4−43）的二维DCT 正变换，产生二维DCT 谱值。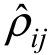

（2）由式（4−47）计算得到。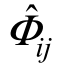

（3）作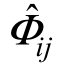的二维DCT 反变换，得到最小二乘意义下的去包裹相位ijΦ。

应当注意，在i=0 和 j=0 处，式（4−47）的分母为零，这意味着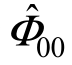是不确定值，因为对常数偏置无法解得Poisson 方程。在实际计算中，可设以使该偏置保持不变。