快速相位提取算法与分析

改进快速相位提取算法的基本出发点均是将移相误差因子ε 作为常数项误差予以消除。但是，当系统采集多组（每组同样帧数）干涉图作累加平均时，ε 的大小是随机变化的，此时，ε 构成的是变量误差，上述两个算法就不适用了。

针对这种情况，本节构造了新的线性相移误差免疫四帧算法及探测器二次非线性响应误差不敏感六帧算法。

1.线性相移误差免疫四帧算法

假定移相器线性误差因子为ε ，则第i 帧相移量为

干涉图光强表达式为

在四幅取样干涉图中，i=0，1，2，3，对前三幅干涉图构造相移算式

对后三幅干涉图有

将式（3−52）代入式（3−51），并令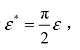有

整理得

上式经整理，可写成

由式（3−54）得

亦可写成

从而

将式（3−54）和式（3−56）代入上式整理，得

上述算法是将相移误差因子ε 解出，不论ε 的大小随机变化如何，都将其作为一中间值考虑进去，最后的相位计算式与线性相移误差因子无关。因此，该算法对线性相移误差是免疫的。(www.xing528.com)

2.探测器二次非线性响应误差不敏感六帧算法

本算法利用五帧算式对探测器二次非线性响应的抑制特性，取六帧干涉图，进行前后两组五帧干涉图的套算。

假定移相器线性相移误差因子为ε，则第k 帧相移量取为

式中，α 为相移量。

干涉图光强表达式为

取六帧干涉图，k=0，1，2，3，4，5，对前五帧干涉图，有

又

对后五幅干涉图，有

又

解得

将上述各式整理得

令

则有

由上式可见，相位计算式与线性相移误差因子ε 无关，当ε 的大小随机变化时，该算法依然适用。