相对论中的杨-米场模拟：揭示引力与标准模型的契合

“规范对称”这个技术名词比“约束系统”来得更普遍是个不幸的现象，因为两者的物理内涵是一样的，但约束系统的语言比规范系统更容易想象及掌握其物理细节。例如，阐述电磁学是一个U（1）局部规范理论，就算对很多专家来说也是抽象得难窥其中奥秘的理论，但如果把电磁学说成是一个约束系统，约束着理论中的电磁场的自由度，使得在时空上每一点都满足电荷守恒的要求便容易明白得多了！几何测量标度（scale）可以自由选取的构想，是由赫尔曼·外尔于1918年首先发展出来。而在量子力学成形后，外尔注意到波函数具有的重新调校标度（rescaling）的对称性，并进而导出了电磁学中的电荷守恒。当今，我们称量子电动力学为一个U（1）“规范不变性”理论。为了解决当时基本粒子的物理问题，杨振宁以及罗伯特·米尔斯（Robert Mills）于1954年引进了非交换性的规范场位势，现在被称为杨-米非阿贝尔（Non-abelian）规范理论，成为了今天标准模型的基石。

量子场论中的量子场的特质是在每一个空间点上都有着无穷多个自由度；如果在这些无穷多个自由度中存在着对称性，那么在每一点上都必须有一些自由度是多余的，而且它们必须没有物理地位。在当代的术语里，为了得到一个规范不变的、有物理意义的单一参数，这意味着这些多余的自由度必须在每一点上都可以被规范处理掉，就像内蕴时间场变量的霍奇分解那样，而这亦说明了为何规范对称性在场论中都必须是局部的。在某种意义上，这个世界必须是规范的，因为世界需要时间进行演化，而且我们日常的经验告诉我们时间必须只是个一维参数，只有规范对称性才能把“时间场算符”中不相干的自由度消除掉。把规范对称视为相位变化下的对称性的传统术语，是个不完整的概念。这仅仅在量子力学中是恰当的，但是当要处理有着无穷多个自由度的量子场算符时，就显得不适当了。

就如同我们先前所强调过的，在量子场理论里，约束理论比规范理论更加贴切。第一类约束于场算符所产生的剩余自由度（规范自由度）之细小改变和规范对称变换所产生的改变是一样的。在那些物理可观测量中是不能够存在那些剩余自由度的。因此，它们不能在对称变换下改变，而必须与第一类约束对易——此即规范不变性。这与处理只有无穷细小的激发态的量子场论的特质是自洽的。

虽然我们可以诠释动量约束所引起的基本变量的变化，与广义无穷小的坐标变换的效应等价，但必须强调：

（1）理论中真正的基础性对称，乃是由约束量的形式及其所对应产生的精确的变换所完全决定，而非借由将要在作用量及哈密顿量中被积分掉的赝（dummy）空间坐标变量的变换来决定。

（2）H在三维微分同胚映射对称变换下所产生的改变乃是动力场在相同坐标上取值的结果。在这个意义上，这与平常所见到的杨－米规范场变换是自洽的，但一般却把杨－米规范场变换天真地看成是“内部的”，而广义相对论变换则被认定为“外部的”，或者是时－空坐标的变换。

其实真正重要的是，其中对称性乃是由理论中的动力场的变换所完全决定，而非借由“导致的坐标变换”所决定，坐标只是个标签，缺乏任何主动的角色。因此单就空间微分同胚映射变换对称性来说，它们就是爱因斯坦理论的规范对称场，这与一般称作“内部的”杨－米规范场完全一样，都是描述相同坐标点上规范对称场的改变。(www.xing528.com)

正确地同时认识到广义相对论其实就是一个规范场理论，以及其根本的动力变量乃来自空间，而并非空时的度规，不仅化解耦合引力到费米子时所面临的问题，也同时揭示了当四维时空在量子扰动下失去其有效性时，要如何超越等距同构（Isometry）、框纤维丛（Frame bundle）、切面对称规范化等概念所扮演的角色。要自洽性地量子化一个量子场论，就无可避免地必须要提供一个可靠的微观因果结构。在一般惯常的杨－米规范量子场论中，场算符间的对易关系乃经由相对于固定背景度规提供的光锥结构（决定了光锥结构乃至于类时、类空与类光的性质）的柯西（Cauchy）初值超曲面来定义。正如惠勒强调过的一样，因为量子引力态不可能无限精确地让峰值在某个经典配置状态中，四维时空只是一个有适用限制的经典概念。因此，我们就不能天真地在量子领域中定义并应用四维框纤维丛这一典范概念。

另一方面，一个自洽的量子引力理论就应该认识到，作为一个真正的规范对称的空间微分同胚映射对称变换的基础性质，乃完全平行杨－米规范对称性质及其基本动力学变量是空间度规的基础性作用，而不是时空度规的重要性。从重整化群的角度来看，量子场在重整化过程中将重新调整结构并由相应的量子场论的固定点的结构细节来将自己融解成更精细的结构，而顶多是半经典的四维时空结构，将最终融解成更基本的结构。

因此，在不存在背景时空的情况下，当务之急乃利用更具基础性的三维空间度规场（而非四维时空）来定义和量子化引力，一如杨－米规范场理论一般，应该期待一个局部哈密顿密度。这个从四维协变对称转化为三维协变对称的根本的观念转变和典范转移，可以在隐含于局部哈密顿密度中，能够自然而然地实现波粒二象性的量子场的色散关系中，得到进一步支持。

迄今为止，要在普遍缺乏等距同构（更不消说洛伦兹等距同构了）的弯曲时空流形中兼容地引入费米子，可以从同构于闵氏时空的切空间的对称群的规范化中实现。在缺乏基本的四维时空和框纤维丛的支持时，我们应该转向利用空间度规或怜三面形（Dreibein）来提供必要和足够的框架。我们在量子化的引力理论中引入费米子物质将要面对的迫切问题就是：当四维度规及有效的半经典四维时空在各种重整化的尺度缩放过程中，融解成更基本的三维空间建构块的度规场和其共轭动量场时，如何将这些基本粒子在各种重整化的尺度缩放过程中保持其“基本”性，而不会在重整化过程中显现出新的结构。

微妙的是，大自然不仅提供了将量子几何动力学视作规范微分同胚映射对称场论时，碰到缺乏基本的四维时空间这一困难局面的解决方案，同时，也启示了耦合量子引力到费米子时乃是规范化三维空间度规的洛伦兹对称群，而不是四维流形上切面空间的闵氏空间的等距同构。怜三面形eia与空间度规的关系是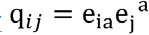，使得空间度规在对怜三面形做局部SO（3，C）群旋转时保持不变。这是一个非凡的事实，即复变数群SO（3，C）实际上是洛伦兹群的另一种表现形式，因为它是与SO（1，3）群同构的。因此，完整的洛伦兹对称性，并不仅仅是实数SO（3）的旋转对称，其实早就已经存在于空间度规中。SO（3，C）和它的覆盖群SL（2，C）的规范化，更是自然而然地让基本的外尔费米子同时兼容着基本粒子物理的标准模型的手征性。

此外，在规范化完整的洛伦兹对称性过程中，我们只需要利用到基本的三维空间怜三面形及其共轭动量，而不需要用到任何四维时空性质。在这层意义上，即使在量子引力的范围，当半经典时空和四维度规失去其适用性时，基本费米子依然可以保持其基本性质。基本费米子的手征性，因此是自动和自洽地通过这个洛伦兹规范对称的方法来实现。最后还必须指出，这与一般在量子力学中的相因子规范不同，在量子场论中的费米子场，虽然是基本的，但它们本身却不是物理态，因此非紧致群的规范化，例如，SL（2，C）并不产生任何异议或者抵触。每当一个明确定义的四维时空出现在经典脉络的情况下，嵌入空间度规的无迹外曲率（extrinsic curvature）都有着清楚的物理诠释，而时空则可以从怜三面形和延聘函数中像前文所提及的时空重建的程序那样，自洽地重建起来。