物理与数学的奇迹：时间起源自量子引力

在人类漫长的文化历史中，睿智和愚庸共存。我们可以想象，任何可以想到的想法都已经被想过了——哥德尔的工作指出广义相对论可能存在缺憾，狄拉克指出时空对称性不应该是引力理论所具有的对称性，惠勒强调三维空间（而非四维时空）的重要性，德威特革命性地提出时间应该由理论内蕴地决定，霍拉瓦即放弃了四维时空对称性引入高次空间导数；所有这些意见都含有部分真理，但都不是真理的全部，但综合先驱们的所有观点后，我们认为以三维空间作为出发点的想法值得我们更深入地进一步分析与了解。

一个配以三维空间度规及其共轭动量（qij，πij）作为基本动力学变量（如同一般正则力学里的坐标X与动量P的推广）的几何动力学理论，承继了一些来自度规值得一提的特征：空间度规的正定性确保了任意初值曲面上两点间的类空性质，并且允许了，用惠勒的话来说，“一个共同一致的‘同时性’的概念，以及初步对‘时间’的感知”。在没有特定背景时空度规（注意，时空是空间演化堆叠而成的古典概念）的量子引力理论中，非度规场的基本变量自身无法生成一个距离的度量，乃至自洽的初值超曲面。给定了一组基本的三维空间度规及其共轭动量后，下一步便是要利用它们来建构一个内蕴时间变量。我们首先要分解三维空间度规成为幺模（Unimodular）因子和行列式因子部分，即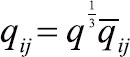（可把qij视为三乘三的矩阵而q就是行列式），而Inq场就是恰好的内蕴时间自由度，也就是之前所提到的与超空间（Superspace，所有三维几何的空间）对应的时间。

狄拉克、惠勒以及霍拉瓦，全都是放弃广义相对论中的时空对称的先驱；我们应当深入了解他们的见解到底是怎么一回事。奇迹般地，下面数个表面看来不太相干的因素，现在却共同催化最简且令人不得不信服具有内蕴时间Inq的量子引力理论之表述。首先，由于Inq是一个物理场，在每一个空间点上都可以拥有不同值，因而不完全符合我们对时间的直觉。但我们应该记住，含有物理意义的不是绝对时刻而是事件间的时间间隔；这时，奇迹再度发生——一个规范不变及合符直觉的时间间隔就唯一地隐藏在Inq场的内蕴时间间隔中，它的平均值就刚好不折不扣地正比于宇宙的部分体积变化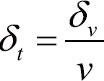。数学上把隐藏在Inq场中的规范不变的时间间隔唯一地确认出来的技术通常称为霍奇分解（Hodge decomposition）。(www.xing528.com)

直观上时间间隔都必须只是一个一维的参数，用来描述演化过程。然而藏有奥妙的是，从一个在所有空间点上都可以拥有不同值的场，要收敛到只剩下一个一维的时间参数，理论中就必须拥有局域规范对称性来收缩成等同的物理。此时H＝0所描述的三维微分同胚映射对称恰好把内蕴时间间隔唯一地确认为宇宙的部分体积变化。这启示了宇宙中最深刻的谜题：为什么宇宙在基本的层次上都需要拥有局部规范对称？因为只有三维微分同胚映射局部规范对称才能允许场自由度坍塌到一个单一的一维参数，好让时间在宇宙中出现。此外，对应到H＝0约束的量子动力演化可巧妙地导出最终规范不变的量子态演化方程——薛定谔方程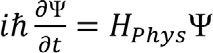：。这就是我们熟悉的、适用于所有物理系统的量子演化方程。

这是一个揭开革命序幕的关键步骤，一个极度重要的突破：量子引力理论现在能够被所对应的一阶的内蕴时间导数之薛定谔方程所支配［伴随着在任何内蕴时刻的半正定（positive semi-definite）概率密度的结论］。这个方案解决了量子力学诠释（这里头需要时间概念与半正定概率密度两者）与通常的克莱恩-戈登（Klein-Gordon）型属于的、二阶内蕴时间导数（因而没有明确的“概率”）之惠勒-德威特方程之间的深度分歧。此外，因为量子演化先后秩序并不对易，薛定谔演化还提供了规范不变的时间排序（因果关系）。“因果”不单是物理也是宗教、伦理学的基础。另一方面，1933年泡利提出一个定理，困扰着有志一探时间真实面目的心灵——泡利证明了不存在着时间的自伴算子，因为时间与哈密顿量共轭的性质会让能量变成连续且无下限。狄拉克在1926年曾提出薛定谔方程乃等同于把相空间（phase space）扩大到包括约束Hphys＝-π在内蕴时间的表述当中，泡利设下的魔咒被奇妙而深刻地克服了——虽然内蕴时间是量子场算符，但哈密顿量并不含内蕴时间t的共轭量π。其中深刻之处在于这些结果都并不需要外加或假设什么条件，而自自然然地从方程式中直接流露出来，而且约束就是以上的薛定谔方程。延伸狄拉克的构想，量子力学里时间的起源乃来自扩大相空间的一个自由度，而量子引力理论就提供了这个唯一的答案。