事件关系、概率计算和组合概率

题型Ⅰ 单因素试验的方差分析

例8.1 要新做一批学生的校服，抽查了某地区三所小学中五年级男生的身高，所得数据如表8.1所示.

表8.1

设男生身高服从具有相同方差的正态分布，当α=0.05时，试问该地区这三所小学五年级男生的平均身高有无显著区别？

解 设第i所小学第j名男生身高为Xij，则Xij～N（μi，σ2）（i=1，2，3；j=1，2，…，6）.

方差分析表如表8.2.

表8.2

因F0.05（2，15）=3.68＜4.3717，故在α=0.05水平下拒绝H0，即认为三所小学五年级男生的平均身高有显著区别.

例8.2 表8.3为某年级三个小班一次数学测验的成绩.

表8.3

试分析三个小班的平均成绩是否有显著差异.

解 记μ1，μ2，μ3为Ⅰ，Ⅱ，Ⅲ三个小班的平均分数，检验假设

H0：μ1=μ2=μ3，H1：μ1，μ2，μ3不全相等.

这里s=3，n1=12，n2=15，n3=13，n=40，所以

方差分析表如表8.4所示.

表8.4

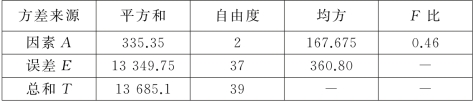
因F0.05（2，37）=3.25＞0.46，故不拒绝H0，认为各班平均分无显著差异.

题型Ⅱ 无重复的双因素方差分析

例8.3 酿造厂有化验员3名，担任发酵粉的颗粒检验，今有3名化验员每天从该厂所产的发酵粉中抽样一次，连续10天，每天检验其中所含颗粒的百分率，结果如表8.5所示.

设α=0.05，试分析3名化验员每日所抽取样本之间有无显著差异？

表8.5

从而得方差分析表如表8.6所示.

表8.6

FA＜Fα=F0.05（2，18），说明FA未落在拒绝域内，故接受H0A，即认为3名化验员的化验技术无显著差异.

FB＞Fα=F0.05（9，18），说明FB落在拒绝域内，故拒绝H0B，即认为每日所抽取的样本之间有显著差异.

题型Ⅲ 有交互作用的双因素方差分析(www.xing528.com)

例8.4 表8.7为温度（因素B）与浓度%（因素A）对种子发芽数的影响.

表8.7

试分析浓度与温度对种子的发芽数是否有显著影响.

解 需检验假设H01、H02、H03，于是

方差来源、平方和、自由度、均方、F比等列于表8.8.

表8.8

故只有浓度的影响是显著的.

题型Ⅳ 一元线性回归分析

例8.5 测得某物质在不同温度下吸附另一种物质的重量见表8.9所示.

表8.9

（1）画出x与y的散点图；

（2）求x与y的一元线性回归方程；

（3）求ε的方差σ2的无偏估计；

（4）检验回归效果是否显著；

（5）求b的置信水平为0.95的置信区间；

（6）求x=0.5处u（x）的置信水平为0.95的置信区间.

解 （1）散点图略.

题型Ⅴ 可化为线性回归的非线性回归分析

例8.6 在彩色显影中，由经验知形成染料光学密度y与析出银的密度x由公式表示，测得实验数据由表8.10所示.

表8.10

题型Ⅵ 多元线性回归分析

例8.7 大豆播种至出苗的长短取决于土壤温度和水分，现有数据如表8.11所示，试建立大豆出苗时间、土壤温度和水分的二元线性回归方程.

表8.11