应用概率论与数理统计同步辅导（第2版）-释难解惑

1.怎样区分互逆事件和互斥事件？

答 事件A与B互斥指的是两者不可能同时发生，而事件A与事件B互逆指的是A与B不但不能同时发生，还需A与B中有一个事件必发生.即

A与B互斥⇔AB=Φ；

A与B互逆⇔AB=Φ且A+B=Ω.

2.样本空间的选取是否唯一？

答 样本空间的选取一般不唯一.在解题的过程中，选取恰当的样本空间，可简化计算，参见例1.11方法二.

3.如何理解概率的公理化定义？

答 前苏联大数学家柯尔莫哥洛夫于1933年成功地将概率论实现公理化.前面我们曾指出：事件与试验相联，试验的每个结果称为事件.与此相应，在柯式的公理化体系中引进一个抽象的集合Ω，其元素ω称为基本事件；一个事件是由若干个基本事件构成的，与此相应，在柯氏的公理化体系中考虑由Ω的子集构成的一个集类F，F中的每个成员就称为“事件”.事件有概率，其大小随事件而异.换言之，概率是事件的函数，与此相应，在柯式的公理化体系中引进一个定义在F上的函数P，对F中的任一成员A，P（A）之值即可理解为概率.柯氏的公理化体系对此函数P加上几条要求（即公理）：

(1)0≤P(A)≤1;

(2)P(Ω)=1,P(Φ)=0;

（3）对于Ω中两两互斥的事件A1，A2，…，An，…都有

我们举一简例说明概率的公理化定义的实现：掷一颗质地均匀的骰子，观察出现的点数.集合Ω={1，2，3，4，5，6}有6个元素构成，反映掷骰子的6个基本结果.作为F，在本例中包括Ω的所有可能子集，故F有26=64个成员，即该随机试验产生64个事件，此时概率函数P定义为

如A={1，2，3}，即表示出现的点数小于4这一随机事件，则

4.不可能事件的概率是0，而概率是0的事件是否一定是不可能事件？

答 由概率的性质知不可能事件的概率是0；但概率是0的事件不一定是不可能事件.例如：在几何概型下，样本空间Ω为区间[0，1]上的随机点构成，事件A={x|x=a}（其中a为区间[0，1]内的某一常数），则P（A）=P{x|x=a}==0，但事件A并不是不可能事件。另外，我们在第二章学习了连续型随机变量的相关知识后也可对此加以说明.

5.P（AB）与P（B|A）有何区别？

答 P（AB）表示事件A与B同时发生的概率，P（B|A）表示在事件A发生的条件下事件B发生的条件概率.它们的计算方法如下：(www.xing528.com)

6.全概率公式和贝叶斯公式适用于哪些问题？

答 全概率公式适用问题的一般特征是：随机试验可分为两个层次，第一层次的所有可能结果A1，A2，…，An构成一个完备事件组，它们通常是第二个层次事件发生的基础或原因；需要求概率的事件是第二个层次中的事件B.而找到完备事件组是运用全概率公式的关键.

贝叶斯公式适用问题的特征与全概率公式相同，只是所求问题为全概率公式的逆问题：已知第二个层次中的事件B发生了的条件下，求第一层次中的事件Aj发生的条件概率，使用公式的关键仍然是找到完备事件组.

7.事件A与B互斥（或互不相容），与事件A与B相互独立的区别和联系是什么？

答 事件A与B互斥即AB=Φ，描述的是两事件的关系，即两者不能同时发生.

事件A与B独立指事件A的发生与否与事件B的发生与否无关，即P（AB）=P（A）P（B）或P（B|A）=P（B）描述的是两个事件的概率关系.

当P（A）＞0且P（B）＞0时，

（1）若A与B独立，则P（AB）=P（A）P（B）＞0，故AB≠Φ，即A与B相容.

（2）若A与B互斥，即P（AB）=P（Φ）=0，而P（A）P（B）＞0，则P（AB）≠P（A）P（B），即A与B不相互独立.

8.n个事件相互独立与两两独立的区别与联系是什么？

答 根据定义，n个事件相互独立需满足=2n-n-1个等式，而两两独立只需满足其中的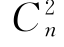个等式即可，故n个事件相互独立一定两两独立，但两两独立不一定相互独立.

例如：已知甲、乙两袋中分别装有编号为1，2，3，4的四个球，今从甲、乙两袋中各取出一球，设A={从甲袋中取出的是偶数号球}，B={从乙袋中取出的是奇数号球}，C={从两袋中取出的都是偶数号球或都是奇数号球}，则A，B，C两两独立但不相互独立.

因为根据题意，P（A）=P（B）=P（C）=，以i，j分别表示从甲、乙两袋中取出球的号数，则试验的样本空间为

由于Ω包含16个样本点，事件AB包含4个样本点（2，1），（2，3），（4，1），（4，3），而AC，BC都各包含4个样本点，故

因此，A，B，C两两独立.

又因为ABC=Φ，所以P（ABC）=0，而P（A）P（B）P（C）=1/8，显然，P（ABC）≠P（A）P（B）P（C），故A，B，C不是相互独立的.