【摘要】：在临界状态下结构新的平衡形式如图所示。设挠曲线方程为：排架的应变能为：外力势能为：结构的总势能：由势能驻值定理：及a1≠0可得：①当n=0时，②当n=1时，③当n=∞时，挠曲线方程为y=a1x2（a-x），则：
【解】 （1）静力法：原结构具有无限个稳定自由度，可简化为如图（a）所示的结构。其中，
。
在临界状态下结构新的平衡形式如图（b）所示。
杆件任一截面的弯矩为：M=-FP·（Δ-y）+FR·（a-x）
由挠曲线近似微分方程：EI1y″=-M=FP（Δ-y）-FR（a-x）
即：EI1y″+FP·y=-kΔ（a-x）+FP·Δ
令
，在上式两边同时除以EI1，得：
设微分方程的通解为：
初始条件为：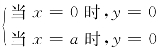
代入后可得：
在临界状态下，A、B 和Δ 不全为0，故系数行列式应为0，即：
将上式展开，并代入FP=α2·EI1，得稳定方程为：
①当n=0时，I2=0，此时可求得：
②当n=1时，I2=I1，此时稳定方程为：
通过试算可得：
(www.xing528.com)
③当n=∞时，I2=∞，此时原结构可简化为图（c）所示结构。
通过试算可得：
（2）能量法：原结构可简化为图（d）所示结构。
在临界状态下，结构新的平衡形式如图（e）所示。
设挠曲线方程为：
排架的应变能为：
外力势能为：
结构的总势能：
由势能驻值定理：
及a1≠0可得：
①当n=0时，
②当n=1时，
③当n=∞时，挠曲线方程为y=a1x2（a-x），则：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
