(a)【解】 该结构为两个自由度体系,用柔度法求自振频率,作![]() 图,分别如图(a)、(b)。
图,分别如图(a)、(b)。
由![]() 图自乘得
图自乘得![]()
![]()
由![]() 图自乘得:
图自乘得:![]()
将![]() 与
与![]() 互乘得:
互乘得:![]()
![]()
由行列式: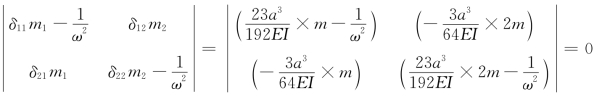
求得自振频率: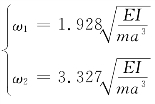
主振型: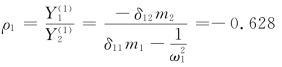
(b)【解】 该结构为两个自由度体系,用柔度法求自振频率,作![]() 图。
图。
由![]() 图自乘得:
图自乘得:![]()
由![]() 图自乘得:
图自乘得:![]() 图互乘得:
图互乘得: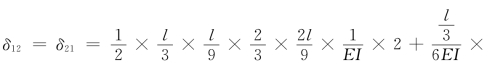
将![]() 与
与![]()
![]()
由行列式: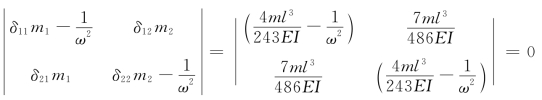
求得自振频率: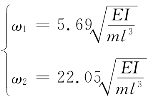
主振型: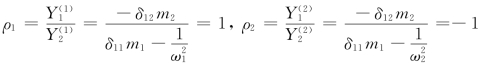
(c)【解】 该结构为两个自由度体系,用柔度法求自振频率,作![]() 图。
图。
由![]() 图自乘得:
图自乘得:![]()
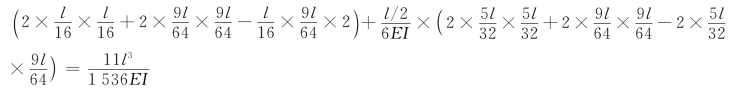
由![]() 图自乘得:
图自乘得:![]()
将![]() 与
与![]() 图互乘得:
图互乘得:![]()
![]()
由行列式: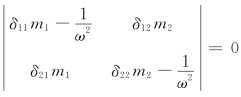 ,求得自振频率为:
,求得自振频率为:![]()
![]()
主振型: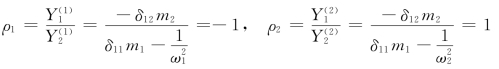
【注解】 本题亦可利用对称性,按正对称和反对称,分别取半结构求解如图(c)、(d)。其中正对称半结构相当于两端固定的梁(忽略轴向变形)。
(d)【解】 该结构为两个自由度体系,用柔度法求自振频率,作![]() 和
和![]() 图。
图。
由![]() 图自乘得:
图自乘得: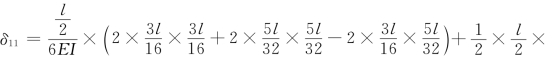
![]()
由![]() 图自乘得:
图自乘得:![]()
![]()
将![]() 与
与![]() 图互乘得:
图互乘得:![]()
![]()
由行列式: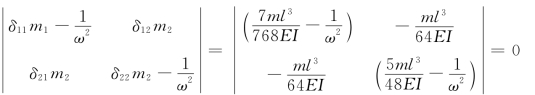
求得自振频率: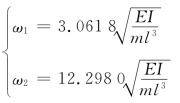
主振型: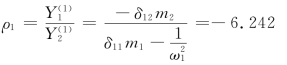
(e)【解】 该结构为两个自由度体系,用柔度法求自振频率,作![]() 图和
图和![]() 图。
图。
由![]() 图自乘得:
图自乘得:![]()
![]()
由![]() 图自乘得:
图自乘得:![]() (https://www.xing528.com)
(https://www.xing528.com)
将![]() 与
与![]() 图互乘得:由其对称性易知:δ12=δ21=0
图互乘得:由其对称性易知:δ12=δ21=0
由行列式: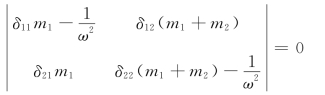
求得自振频率为:
【注解】 ①由以上分析可知,δ12=δ21=0,说明两个振动微分方程不是耦合的而是独立的,也就是说水平振动与竖向振动互不影响,各自作独立的自振。求振型时,不能简单套用振型计算公式,否则会出现0/0的错误结果。由于两个方向的振动互不影响,因此当发生水平振动时,竖向不振动,第一振型ρ1=1/0;发生竖向振动时,水平不振动,第二振型ρ2=0/1。
②系数δ12、δ22应与(m1+m2)相乘,表示参与该方向振动的质量之和。
(f)【解】 该结构为三个自由度的体系,用柔度法求自振频率,作![]() 图,分别如图(a)、(b)、(c)。
图,分别如图(a)、(b)、(c)。
由图自乘得:![]()
![]()
由![]() 图自乘得:
图自乘得:![]()
由![]() 图自乘得:
图自乘得:![]()
将![]() 与
与![]() 图互乘得:
图互乘得:![]()
将![]() 与
与![]() 图互乘得:δ13=δ31=0
图互乘得:δ13=δ31=0
将![]() 与
与![]() 图互乘得:δ23=δ32=0
图互乘得:δ23=δ32=0
由行列式:
求得自振频率为:![]()
主振型:![]()
(g)【解】 该结构为两个自由度的体系,用柔度法求自振频率,作![]() 和
和![]() 图,分别如图(a)、(b)。
图,分别如图(a)、(b)。
由![]() 图自乘得:
图自乘得:![]()
由![]() 图自乘得:
图自乘得:![]()
![]()
将![]() 图与
图与![]() 图互乘得:
图互乘得:![]()

由行列式:
求得自振频率为: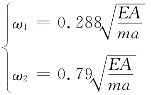
主振型:
(h)【解】 该结构为两个自由度体系,用柔度法求自振频率,作![]() 和
和![]() 图。
图。
由![]() 图自乘得:
图自乘得:![]()
由![]() 图自乘得:
图自乘得:![]()
将![]() 与
与![]() 图互乘得:
图互乘得:![]()
由行列式:
求得自振频率为: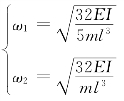
主振型: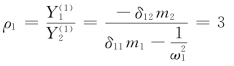
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




