振动体系对称分析与最大位移、自振频率、放大系数和弯矩图

在结构动力学中，振动体系的对称性是指结构和质量均对称分布。对称振动体系具有如下特点：

自由振动：振型为正对称和反对称，分别对两种振型取半结构计算。

强迫振动：可将动荷载分解成正对称和反对称两组；正对称荷载作用下，振型表现为正对称；反对称荷载作用下，振型表现为反对称，分别计算后再进行叠加。如图10-12（a）所示的体系，自由振动时可分解为图10-12（b）、（c）所示的正对称半结构和反对称半结构两种情况。

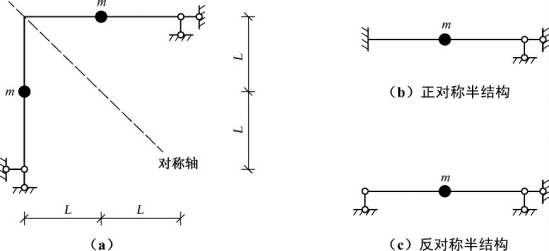
图10-12

【例10-5】　图10-13所示结构的EI=107N·m2，L=10m，m=2　000kg，θ=0.5ω。

（1）求图示结构的自振频率和振型；

（2）求图示结构在P（t）=80kN·sinθt 作用下的位移响应，不考虑阻尼。（东南大学2009）

图10-13

【解】　（1）原结构为对称结构，自由振动时振型可分为正对称和反对称，分别对两种振型取半结构分析。

图10-14

①正对称情况：半结构为单自由度体系，作图，如图10-14（a）所示。

柔度系数：

自振频率：

由于第一振型为正对称的，故。(https://www.xing528.com)

②反对称情况：半结构为单自由度体系，作图，如图10-14（b）所示。

柔度系数：

自振频率：

由于第二振型为反对称的，故。

（2）在动荷载P（t）作用下，原结构作正对称的强迫振动，取半结构分析，如图10-15（a），由（1）可知：正对称半结构为单自由度体系，图如图10-14（a）所示，作MP图，如图10-15（b）。

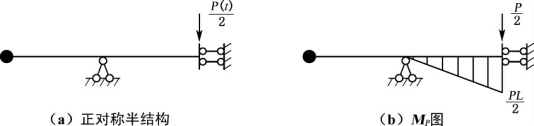
图10-15

强迫振动微分方程：

由（1）知：，拟静位移：

自振频率：，动力放大系数：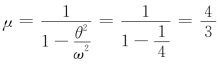

质点处的最大位移：

惯性力幅值：

作结构的最大弯矩图，如图10-16所示。

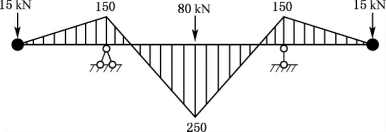
图10-16　最大弯矩图（kN·m）

【注】　最大弯矩图中作用在质点上的15kN为惯性力幅值-5kN（↑）与质点自重mg=20kN（↓）的叠加，方向向下。