动荷载作用下的最大动位移及最大动弯矩图

以单自由度体系在简谐荷载作用下（设为FP（t）=Psinθt）的无阻尼强迫振动为例，根据动荷载是否作用在质点上，分以下两种情况讨论。

（1）当FP（t）=Psinθt不作用在质点上时：

①振动微分方程：，式中Δ1P由与MP图乘所得。

②最大动位移（振幅）：A=μyst=μΔ1P。

③动位移放大系数μ 与动内力放大系数μ′不相等。

④最大动弯矩图：将动荷载幅值和惯性力幅值同时作用在结构上，可得最大动弯矩图（这是作最大动弯矩图的通用方法）。

（2）当FP（t）=Psinθt作用在质点上时：

①振动微分方程：。

②最大动位移（振幅）：A=μyst=μPδ11（此时Δ1P=Pδ1P=Pδ11）。

③动位移放大系数μ 与动内力放大系数μ′相等。

④最大动弯矩图：此时除了采用上述介绍的通用方法以外，由于已求得动内力放大系数，最大动弯矩值可利用动内力放大系数求解，即：Mmax=μMst。

式中：Mst——动荷载幅值P 引起的拟静弯矩值，即MP图。

【注意】

①μ 的值可正可负，其取值范围为：（-∞，0）和（1，+∞）。

②惯性力幅值也可正可负。若为正值，表明惯性力幅值与图中单位荷载的方向相同，即惯性力与动荷载频率相同；若为负值，表明惯性力幅值与图中单位荷载的方向相反，即惯性力与动荷载频率相反。

【例10-3】　试求图10-6所示结构在动荷载作用下，悬臂端的最大动位移，并作该结构的最大动弯矩图。已知：各杆EI=常数，θ=0.5ω。（东南大学2014）

图10-6

【解】　本例为单自由度体系的无阻尼强迫振动，采用柔度法求结构的自振频率，分别作和MP图，如图10-7（a）、（b）。

图10-7

柔度系数：

拟静位移：(www.xing528.com)

自振频率：

动位移放大系数：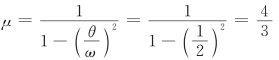

悬臂端的最大动位移（振幅）：

惯性力幅值：

将惯性力幅值和动荷载幅值同时作用在结构上，作出最大动弯矩图，如图10-8。

图10-8　最大动弯矩图

【例10-4】　试求图10-9（a）所示结构在动荷载FP（t）=FPsinθt作用下柱顶的最大动位移，并作最大动弯矩图，已知。（同济大学2001）

图10-9

【解】　本例属单自由度体系的强迫振动问题，采用刚度法求体系的自振频率，当柱顶发生单位侧移时的弯矩图如图10-9（b）所示。

由图10-9（b）可得，，故自振频率为：。

作结构在FP作用下的MP图，可根据第7章中的剪力分配法，即分解成“锁住”和“松开”两种状态，如图10-10（a）、（b）和（c）所示。

图10-10

求拟静位移时，可将MP图与原结构的任一种基本结构的单位弯矩图相乘，这里选取如图10-11（a）所示较简单的基本结构。

拟静位移：；

动力放大系数：；　振幅：；

图10-11

惯性力幅值：。

将惯性力幅值和动荷载幅值同时作用在结构上，作最大动弯矩图，如图10-11（b）、（c）（注：最大动弯矩图的求解亦可采用与作MP图相同的处理方法）。