(a)【解】 结构标识如下图所示,用后处理法求解结构的总刚度方程。
(1)单元分析:
单元①: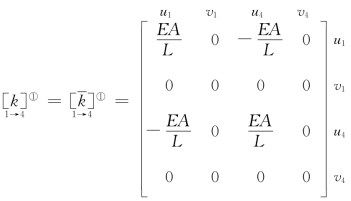
单元②:![]()
单元③:α=90°,cosα=0,sinα=1
单元④:![]()
单元⑤:α=0°,无需进行坐标转换
单元⑥:α=270°,cosα=0,sinα=-1
(2)整体分析:用直接刚度法集成结构的原始总刚[KP]
(3)引入边界条件:u1=v1=u2=v2=0,删去原始总刚[KP]中的第1、2、3、4行(列),得到结构的总刚度矩阵:
(4)综合结点荷载向量:[F]=[Fx3,Fy3,Fx4,Fy4]T=[20kN,0,0,-20kN]T
未知结点位移向量:[Δ]=[u3,v3,u4,v4]T
总刚度方程:[F]=[K]·[Δ],即:
(5)解方程可得:![]()
(6)求各杆端力:
单元①: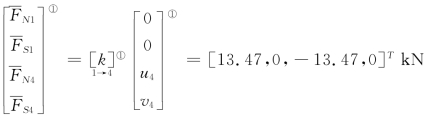
单元②:
单元③: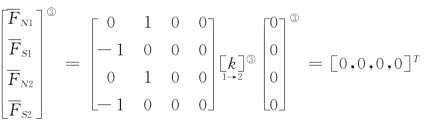
单元④: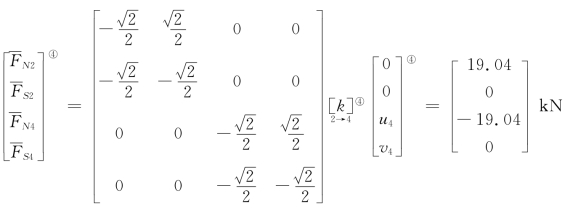
单元⑤: (https://www.xing528.com)
(https://www.xing528.com)
单元⑥: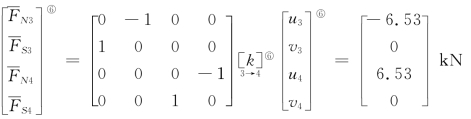
各杆的轴力如下图所示,以受拉为正,受压为负。
(b)【解】 结构标识如图(a)所示,用后处理法求解结构的总刚。
(1)单元分析:
单元①:
单元②:α=90°,cosα=0,sinα=1
单元③:![]()
(2)整体分析:用直接刚度法集成结构的原始总刚[KP]
(3)引入边界条件:u2=v2=u3=0,故删去原始总刚[KP]中的第3、4、6行(列),得到结构的总刚度矩阵:
(4)综合结点荷载向量:[F]=[Fx1,Fy1,Fx3]T=[FP,0,0]T
未知结点位移向量:[Δ]=[u1,v1,u3]T
总刚度方程:[F]=[K][Δ],即:
(5)求解方程可得:![]()
(6)求各杆端力:
单元①: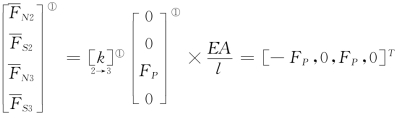
单元②: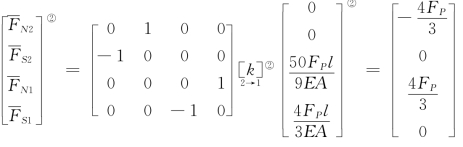
单元③:
从而得到:FN23=FP(受拉),![]() (受拉),
(受拉),![]() (受压)
(受压)
各杆轴力如图(b)所示,以受拉为正,受压为负。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




