【摘要】:单元分析:整体分析:用直接刚度法集成原始总刚[KP]引入边界条件:θ1≠0,θ2≠0,θ3≠0,θ4≠0,故结构的总刚[K]=[KP]结点和单元编号如下图所示,原结构为多跨连续梁,只考虑弯曲变形,且局部坐标系与整体坐标系相同,无需进行坐标转换。
(a)【解】 结点和单元编号如下图所示,原结构为多跨连续梁,无需进行坐标变换,且只考虑杆件的弯曲变形。
(1)单元分析: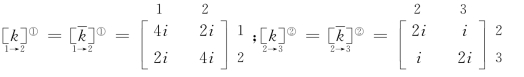
(2)整体分析:用直接刚度法集成原始总刚[KP]
(3)引入边界条件:θ1≠0,θ2≠0,θ3≠0,θ4≠0,故结构的总刚[K]=[KP]
(b)【解】 结点和单元编号如下图所示,原结构为多跨连续梁,只考虑弯曲变形,且局部坐标系与整体坐标系相同,无需进行坐标转换。
(1)单元分析: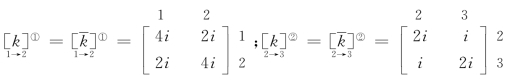 ;
;
(2)整体分析:用直接刚度法集成结构的原始总刚[KP]
(3)引入边界条件:θ1=θ4=0,θ2≠0,θ3≠0,故删去原始总刚中第1、4行(列),得到结构的总刚度矩阵为:![]()
(c)【解】 结构标识如下图,原结构杆件刚度有变化,故需考虑刚度变化处的横向位移。
(1)单元分析: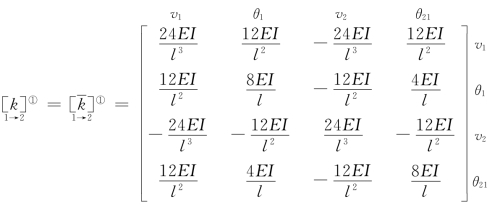
(2)整体分析:用直接刚度法集成结构的原始总刚[KP](https://www.xing528.com)
(3)引入边界条件:v1=θ1=v3=v4=0,删去原始总刚中的第1、2、6、8行(列),得到结构的总刚度矩阵。
故有:
【注解】 若连续梁存在中间铰,则中间铰结点左、右两侧截面的转角位移应分别进行编号,而线位移则用同一编号,在集成原始总刚时应注意正确地“对号入座”。
(d)【解】 结构标识如下图所示,由于杆件刚度有变化,故需考虑刚度变化处的横向位移。
(1)单元分析: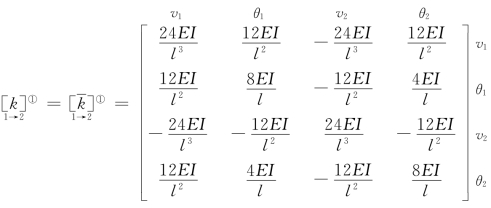 ;
;
(2)整体分析:用直接刚度法集成结构的原始总刚[KP]
(3)引入边界条件:v1=θ1=v3=v4=0,删去以上原始总刚[KP]中的第1、2、5、7行(列),得到结构的总刚度矩阵[K]
故有:
【注解】 若梁中存在刚度变化的杆件,则在刚度变化处应考虑剪切变形。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




