首先将各单元在整体坐标系下的单元刚度矩阵，按结点编号表示成分块形式，然后按“对号入座”原则进行“搬家”，便可形成结构的总刚度矩阵，即直接刚度法。
【注意】
①若某个结点上有多个单元相连，则该结点称为公共结点。若某两个结点之间有单元相连，称该结点为相关结点，反之为非相关结点。与公共结点对应的总刚度矩阵中的子块由各单元刚度矩阵的相应子块叠加，非相关结点之间没有刚度贡献，为零子块。
②当采用先处理法建立总刚度矩阵时，由于各单元已考虑两端的边界条件，因此集成的总刚即为结构最终的总刚度矩阵。而当采用后处理法建立总刚度矩阵时，由直接刚度法形成的是原始总刚度矩阵，还需引入边界条件删去与零位移对应的行（列）后，方可获得最终的总刚度矩阵。
③结构的原始总刚度矩阵具有对称性和奇异性，而最终的总刚度矩阵具有对称性和非奇异性。
【例9-1】 若按图9-1中的结点和单元编号以及指定的坐标系，用后处理矩阵位移法求解该刚架时，在单元②的刚度矩阵中，第5行第2列的那个元素的值为：________（各杆的EI 为常量）。运用直接刚度法，应将该元素送至结构的原始总刚度矩阵中的第_________行、第________列；在引入结构的边界条件时，应删除原始总刚度矩阵中的_____________行和列。（东南大学2014）
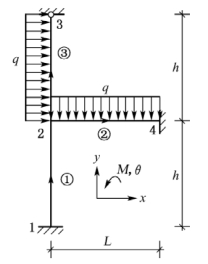
图9-1
【解】 由于单元②的局部坐标方向与整体坐标系一致，故：
第5行第2列元素值为：
；该结构有四个结点，由后处理法建立的原始总刚为12阶矩阵，②号单元的刚度矩阵中第5行第2列元素，位于原始总刚中的3阶子块［k］42中的第2行第2列，即在原始总刚中位于第11行第5列；引入边界条件：u1=v1=θ1=u3=v3=u4=v4=θ4=0，故应删去原始总刚中的第1，2，3，7，8，10，11，12行和列。
（2）综合结点荷载向量
建立总刚度方程的依据是结点平衡条件，当结构上不仅作用有结点荷载，还作用有非结点荷载时，必须将非结点荷载转换为等效结点荷载。整个结构的综合结点荷载向量为：
式中：
——直接结点荷载向量；
——等效结点荷载向量，且有｛FE｝=-｛Ff｝e；
——单元的固端力向量。
【注意】 求各单元的固端力向量以及等效结点荷载向量时，各单元均视为两端固定的单跨超静定梁。(www.xing528.com)
（3）最终杆端内力
各单元的最终杆端内力，为固端力与综合结点荷载下的杆端力之和，即：
或
。求得各单元在局部坐标系下的杆端力后，便可利用区段叠加法作最终内力图。
【例9-2】 按图9-2所示的结构编码，各杆的截面尺寸为b×h=0.25m×0.5m，杆长L=5m，E=3×107kPa。已求得结点位移为：
。试用矩阵位移法求各单元的杆端力，并作内力图。
图9-2
【解】 （1）求各单元在局部坐标系下的单元刚度矩阵：
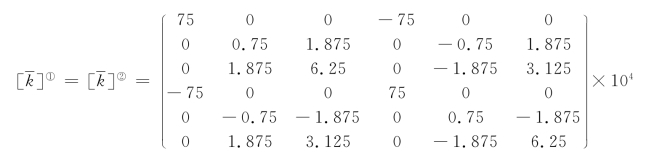
（2）各单元的杆端位移向量：
单元①：α=-60°，cosα=0.5，sinα=-0.866
故有：
单元②：
（3）各单元杆端力向量：
单元①：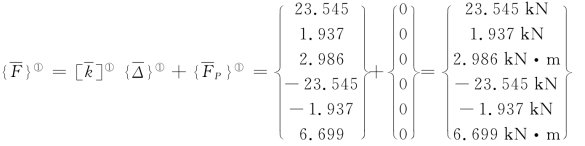
单元②：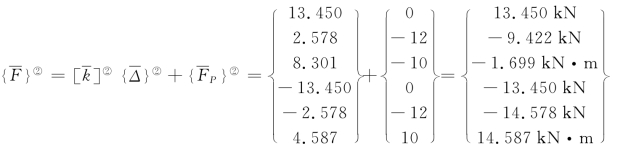
（4）根据各单元的杆端力向量，作内力图，如图9-3所示。
图9-3
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
